পাঠ্য বইয়ের নিয়ম ছাড়া অন্যভাবে ত্রিকোণমিতিক অনুপাতের মান নির্ণয় করা শিখি

আমরা নবম-দশম শ্রেণির পাঠ্য বইয়ে ত্রিকোণমিতিক অনুপাত নির্ণয় করার জন্য একটি পদ্ধতি দেওয়া আছে। আমি তোমাদের অন্যভাবে এই তালিকাটি নির্ণয়করা দেখাবো। তবে এর জন্য আমাদের শুধু তিনটি ত্রিভুজ মনে রাখতে হবে।

তাহলে চলো আমরা একটি একটি করে ত্রিভুজ দেখি এবং এই ত্রিভুজ গুলো ব্যবহার করে কিভাবে ত্রিকোণমিতিক মান নির্ণয় করা যায় তা দেখি ও শিখি-

প্রথমে আমরা 30° ও 60° কোণের ত্রিকোণমিতিক অনুপাতগুলোর মান নির্ণয় করা দেখি:

প্রথমে নিচের চিত্র-১ লক্ষ্য করি।

চিত্র-১

আমরা জানি সমকোণের বিপরীত বাহুই অতিভূজ। সুতরাং অপর দুইটি বাহুর একটি লম্ব অপরটি ভুমি।

চিত্র-১ এ দেখা যাচ্ছে ভূমি সংলগ্ন ∠C=30°। সুতরাং এই অবস্থায় 𝜭 মান 30°। অর্থাৎ ভূমি BC=√3, লম্ব AB=1, অতিভুজ AC=2।

এখন যদি আমরা চিত্র-১ এর ত্রিভুজটিকে নিচের চিত্র-২ এর মত উল্টো করে রাখি, তখন কেমন দেখায় দেখুন তো-

চিত্র-২

এখন ∠A=60° নিচে নেমে গেলো এবং এই অবস্থায় ভুমি AB=1 হয়ে গেলো, লম্ব হয়ে গেলো BC=√3। অর্থাৎ চিত্র-১ এ যেটা ছিলো লম্ব চিত্র-২ এ সেটা হয়ে গেলো ভূমি এবং যেটা ছিলো ভূমি সেটা এখন লম্ব। যেহেতু এখন ভূমির সংলগ্ন ∠A=60°। সুতরাং এই অবস্থায় 𝜭 -এর মান 60°।

আমরা জানি,

চিত্র-১ অনুসারে, যখন 𝜭=30°। তখন লম্ব, ভূমি, অতিভুজ অনুসারে লম্বকে অতিভুজ দ্বারা ভাগ করলে পাই-

একই ভাবে 𝜭=30°র অন্যান্য ত্রিকোণমিতিক অনুপাতের মান হবে-

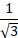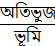এবং চিত্র-২ অনুসারে 𝜭=60° হলে; তখন লম্ব, ভূমি, অতিভুজ অনুসারে পাই-

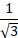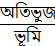এখন 𝜭=45° হলে নিচের চিত্র-৩ এর মত হবে-

চিত্র-৩

এখন আবার চিত্রটিকে যদি উল্টো করে রাখি তবে নিচের চিত্র-৪ এর মত হবে-

চিত্র-৪

অথাৎ চিত্র-৩ ও চিত্র-৪ এর মধ্যে লম্ব ও ভূমির মানের কোনো পরিবর্ত নাই এমনকি দুই ক্ষেত্রেই ভূমি সংলগ্ন কোণের মানেরও পরিবর্তন হয়নি। তাই যেকোন একটা চিত্র ধরেই আমার 𝜭=45° কোণের ত্রিকণমিতিক অনুপাতের মান নির্ণয় করতে পারি।

আর বাকি রইলো 0° ও 90° -এর ত্রিকোণমিতিক অনুপাতের মান। তাহলে নিচের চিত্র-৫ লক্ষ্য করি-

চিত্র-৫

দেখা যাচ্ছে ∠C=0°। এখানে বলে রাখি, 0° হলেতো কোণটির দৃশ্যমান অস্তিত্ব থাকার কথা নয়। যুক্তির খাতিরে আমরা এর একটি কাল্পনিক অস্তিত্ব ধরে নিই। এবং ∠C যেহতু শূন্য তার বিপরীত বাহুও থাকার কথা নয় তাই লম্বেরও দৃশ্যমান অস্তিত্ব থাকবে না। তাও এর একটি দৃশ্যমান অভয়ব ধরে নিলাম। এবং ∠A =90° কারণ, আমরা জানি ত্রিভুজের তিন কোণের সমষ্টি=180°। যেহেতু ∠B=90°, ∠C=0° সুতরাং 180° হওয়ার জন্য অবশ্যই ∠A=90° হতে হবে। এটিরও আমরা একটি কাল্পনিক অস্তিত ধরে নিই। আসলে এই ত্রিভুজটি একটি সরল রেখাংশ ছাড়া আর কিছুই নয়। যার A ও B বিন্দু বস্তুত একই বিন্দু।

চিত্র-৫ অনুসারে ভূমি সংলগ্ন ∠C যেহেতু 0°। তাহলে 𝜭=0° কোণের ত্রিকোণমিতিক অনুপাতগুলো হবে-

বলে রাখি, যেকোনো সংখ্যাকে 0 দ্বারা ভাগ করলে কোনো সঙ্গা বা মান পাওয়া যায় না। তাই 0 দ্বারা ভাগ অসঙ্গায়িত।

এখন এই কাল্পনিক চিত্র-৫ কে যদি আমরা উল্টো করে রাখি তবে চিত্র-৬ এর মত দেখাবে

চিত্র-৬

এখন চিত্র-৫ এ যেটা ছিলো ভুমি এখন চিত্র-৬ এ সেটা লম্ব এবং যেটা ছিলো লম্ব এখন সেটা ভূমি।

সুতরাং এই অবস্থায় ভূমি সংলগ্ন ∠A যেতেহু 90° তাই 𝜭=90° কোণের ত্রিকোণমিতিক অনুপাত গুলো হলো-

এখন উপরের সকল ডিগ্রির ত্রিকোণমিতিক অনুপাতের মান এক তালিকায় দেখি-

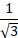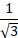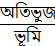সুতরাং মনে রাখতে হবে উল্টানের আগের স্বাভাবিক তিনটি চিত্র। যথা, চিত্র-১, চিত্র-৩, চিত্র-৫ বাকি গুলো বাদ কারণ ওরা আসলে এই তিনটি চিত্রর উল্টো অবস্থা। এদেরকে একবার সোজা করে চিন্তা করে আবার উল্টো করে চিন্তা করে মানগুলো নির্ণয় করেছি।

এখন আমরা মান থকের ত্রিকোণমিতক অনুপাতের নাম ও ডিগ্রি নির্ণয় দেখবা:

ধরো আমি যদি তোমাকে বলি  কো থিটার কত ডিগ্রি হবে। তুমি উপরের তালিকার দিকে না তাকিয়ে কি ভাবে নির্ণয় করবে?

যেহেতু এখানে √3 এবং 2 আছে। তাহলে সকল চিত্রের মধ্যে শুধু মাত্র চিত্র-১ ও চিত্র-২ এই এদের পাওয়া যায়। এবং এই দুইটি চিত্রে অতিভুজ সব সময়ই 2 সুতরাং  ভগ্নাংশের হর 2 অবশ্যই “অতিভুজ” এবং চিত্র-১ অনুসারে √3 ভূমি তখন ভূমি সংলগ্ন কোণ 30°=𝜭 সুতরাং

 আবার যেহেতু চিত্র-২ এ √3 লম্ব তখন ভূমি সংলগ্ন কোণ হয় 60°=𝜭। অথাৎ তখন

একই ভাবে শুধু 0, 1, 2, √2 বা √3 এর ত্রিকোণমিতিক অনুপাতের কোন থিটার কত ডিগ্রি হবে তা নির্ণয়ের জন্য এরদের হর 1 ধরে নিতে হবে এবং ভাবতে হবে কোন কোন চিত্রে বাহুতে 0 আছে, বা 1 আছে বা 2 আছে বা √2 আছে বা √3 আছে। তখন কল্পনায় পাওয়া চিত্রের হর ও লবের মান বহুগুলোর নাম ধরে থিটার নাম নির্ণয় করতে হবে এবং তখন তাদের ভূমি সংলগ্ন কোণ কত ডিগ্রি তা দিয়ে 𝜭 কত হবে তা নির্ণয় করা যায় উপরের উদাহরণটির মত।

*অসঙ্গায়িতের ক্ষেত্রে হর 0 ধরতে হবে।

ট্রিপস্:

যদি কোনো ভগ্নাংশে 2, √2, √3; এদের দেখা যায় সাথে সাথে নিচের এই ত্রিভুজ গুলো মাথায় আসতে হবে। কারণ-

2 ⇒ (45°) ওয়ালা ত্রিভুজ এবং (30°-60°) ওয়ালা ত্রিভুজেই আছে

√2 ⇒ শুধু (45°) ওয়ালা ত্রিভুজেই আছে

√3 ⇒ শুধু (30°-60°) ওয়ালা ত্রিভুজেই আছে

কোনো অনুপাতের মান 1 হতে পারে (45°)  ও (0°-90°) ওয়ালা ত্রিভুজে।

0 ও  অসঙ্গায়িত হতে পারে (0°-90°) ওয়ালা ত্রিভুজে।