৮ম শ্রেণি : এ্যাসাইনমেন্ট : গণিত : ৩য় সপ্তাহ
এ্যাসাইনমেন্ট বা নির্ধারিত কাজের ক্রম :
অ্যাসাইনমেন্ট বা নির্ধারিত কাজ - ১
এ্যাসাইনমেন্ট বা নির্ধারিত কাজ
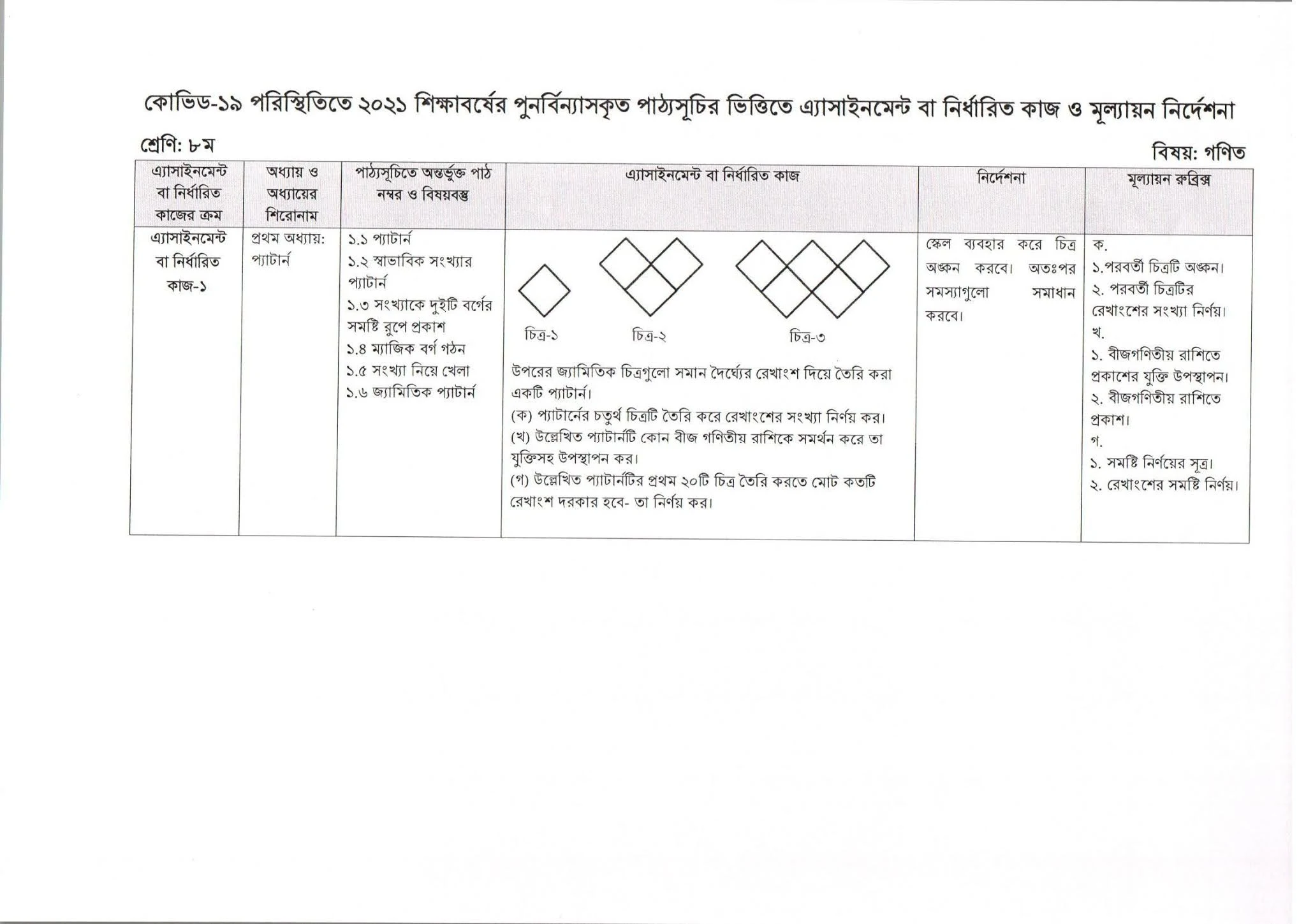
(ক) প্যাটার্নের চতুর্থ চিত্রটি তৈরি করে রেখাংশের সংখ্যা নির্ণয় কর।
(খ) উল্লেখিত প্যাটার্নটি কোন বীজ গণিতীয় রাশিকে সমর্থন করে তা যুক্তিসহ উপস্থাপন কর।
(গ) উল্লেখিত প্যাটার্নটির প্রথম ২০টি চিত্র তৈরি করতে মোট কতটি রেখাংশ দরকার হবে- তা নির্নয় কর।
৮ম শ্রেণির ৩য় সাপ্তাহের অ্যাসাইনমেন্ট-এর গণিত প্রশ্ন দেয়া হলো :
নমুনা সমাধান
(ক) প্যাটার্নের চতুর্থ চিত্রটি তৈরি করে রেখাংশের সংখ্যা নির্ণয় কর।
নমুনা সমাধান :
|
| চতুর্থ চিত্র |
(খ) উল্লেখিত প্যাটার্নটি কোন বীজ গণিতীয় রাশিকে সমর্থন করে তা যুক্তিসহ
উপস্থাপন কর।
নমুনা সমাধান :
প্রথম চিত্রে রেখাংশ আছে ৪ টি = (৬✕১) - ২ = ৪টি
দ্বিতীয় চিত্রে রেখাংশ আছে ১০টি = (৬✕২) - ২ = ১০টি
তৃতীয় চিত্রে রেখাংশ আছে ১৬টি = (৬✕৩) - ২ = ১৬টি
সুতরাং ‘ক’ তম চিত্রে রেখাংশ আছে = (৬✕ক) - ২ টি
উল্লেখিত প্যাটার্নটি (৬ক - ২) বীজগণিতীয় রাশিকে সমর্থন করে।
(গ) উল্লেখিত প্যাটার্নটির প্রথম ২০টি চিত্র তৈরি করতে মোট কতটি রেখাংশ
দরকার হবে- তা নির্নয় কর।
নমুনা সমাধান :
‘খ’ নং প্রশ্নের সমাধান হতে পাই,
প্যাটার্নটির বীজগণিতিয় রাশি (৬ক - ২)
প্রথম চিত্রে রেখাংশ আছে ৪ টি।
২০তম চিত্রে রেখাংশের সংখ্যা হবে (৬✕২০) - ২ = ১২০ - ২ = ১১৮টি।
সুতরাং প্রথম ২০টি চিত্রের মোট রেখাংশের সংখ্যা হবে,
(প্রথম সংখ্যা + শেষ সংখ্যা) ✕ পদ সংখ্যা
⁄
২
$= \frac{\left (৪+১১৮\right )\times ২০}{২}$
$= \frac{১২২\times ২০}{২}$
$= \frac{২৪৪০}{২}$
$= ১২২০$
সুতরাং প্রথম ২০টি চিত্র তৈরি করতে মোট রেখাংশ দরকার হবে ১২২০টি।
আরো দেখুন :
৪র্থ সপ্তাহের নমুনা সমাধান :
৩য় সপ্তাহের অন্যান্য বিষয়ের নমুনা সমাধান :