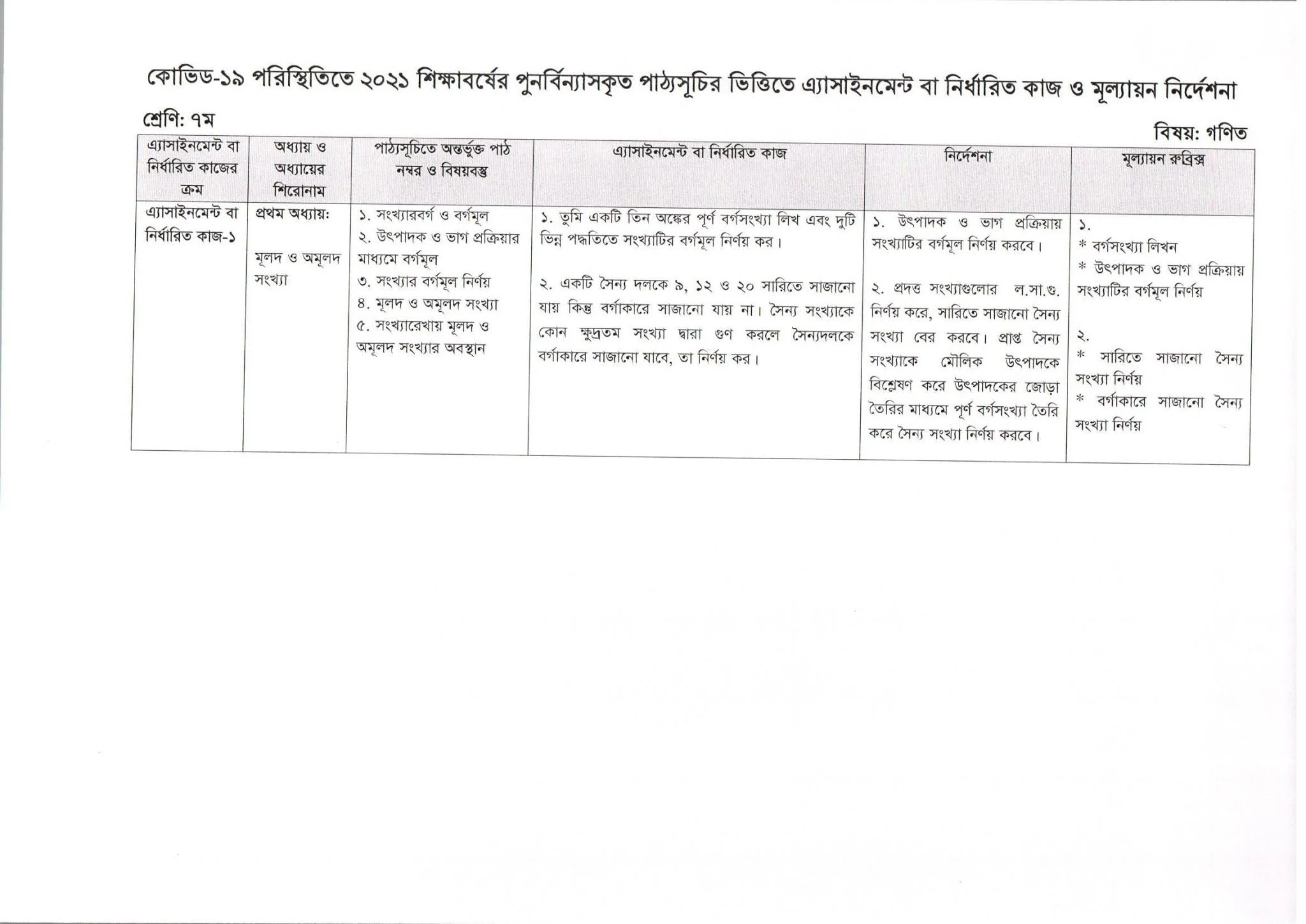
৭ম শ্রেণি : এ্যাসাইনমেন্ট : গণিত : ৩য় সপ্তাহ
এ্যাসাইনমেন্ট বা নির্ধারিত কাজের ক্রম :
অ্যাসাইনমেন্ট বা নির্ধারিত কাজ - ১
এ্যাসাইনমেন্ট বা নির্ধারিত কাজ
১. তুমি একটি তিন অঙ্কের পূর্ণ বর্গসংখ্যা লিখ এবং দুটি ভিন্ন পদ্ধতিতে
সংখ্যাটির বর্গমূল নির্ণয় কর।
২. একটি সৈন্য দলকে ৯, ১২ ও ২০ সারিতে সাজানো যায় কিন্তু বর্গাকারে সাজানো যায় না। সৈন্য সংখ্যাকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুন করলে সৈন্যদলকে বর্গাকারে সাজানো যাবে, তা নির্ণয় কর।
২. একটি সৈন্য দলকে ৯, ১২ ও ২০ সারিতে সাজানো যায় কিন্তু বর্গাকারে সাজানো যায় না। সৈন্য সংখ্যাকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুন করলে সৈন্যদলকে বর্গাকারে সাজানো যাবে, তা নির্ণয় কর।
৭ম শ্রেণির ৩য় সাপ্তাহের অ্যাসাইনমেন্ট-এর গণিত প্রশ্ন দেয়া হলো :
নমুনা সমাধান
১. তুমি একটি তিন অঙ্কের পূর্ণ বর্গসংখ্যা লিখ এবং দুটি ভিন্ন পদ্ধতিতে
সংখ্যাটির বর্গমূল নির্ণয় কর।
নমুনা সমাধান :
মনে করি, তিন অঙ্কের পূর্ণ বর্গ সংখ্যা ১৪৪।
মৌলিক গুণনিয়ক পদ্ধতিতে বর্গমূল নির্ণয় :

১৪৪ এর গুণনিয়ক = (২✕২) ✕ (২✕২) ✕ (৩✕৩)
সুতরাং ১৪৪ এর বর্গমূল = ২ ✕ ২ ✕ ৩ = ১২
ভাগ প্রক্রিয়ায় বর্গমূল নির্ণয় :
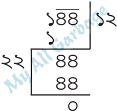
সুতরাং ১৪৪ এর বর্গমূল = ১২
২. একটি সৈন্য দলকে ৯, ১২ ও ২০ সারিতে সাজানো যায় কিন্তু বর্গাকারে সাজানো
যায় না। সৈন্য সংখ্যাকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুন করলে সৈন্যদলকে
বর্গাকারে সাজানো যাবে, তা নির্ণয় কর।
নমুনা সমাধান :
সৈন্য দলকে ৯, ১২ ও ২০ সারিতে সাজানো যায়। কিন্তু বর্গাকারে সাজানো যায় না।
সুতরাং নির্ণয় করতে হবে সংখ্যাগুলোকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুণ করলে
বর্গাকারে সাজানো যাবে।

৯, ১২ ও ২০ এর ল.সা.গু. = (২✕২) ✕ (৩✕৩) ✕ ৫ = ১৮০
যেতেহু ৫ জোড় বিহীন, তাই ১৮০ এর সাথে যদি সর্বনিম্ন ৫ গুণ করে দেয়া হয় তবে একটি পূর্ণবর্গ সংখ্যা পাওয়া যাবে।
সুতরাং সংখ্যাগুলোকে সর্বনিম্ন ৫ দ্বারা গুণ করলে বর্গাকারে সাজানো যাবে।
আরো দেখুন :
৪র্থ সপ্তাহের নমুনা সমাধান :
৭ম শ্রেণি : অ্যাসাইনমেন্ট : চারু ও কারুকলা
৩য় সপ্তাহের অন্যান্য বিষয়ের নমুনা সমাধান :