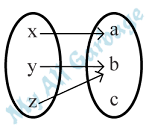৯ম শ্রেণি : এ্যাসাইনমেন্ট : উচ্চতর গণিত : ৩য় সপ্তাহ
এ্যাসাইনমেন্ট বা নির্ধারিত কাজের ক্রম :
অ্যাসাইনমেন্ট বা নির্ধারিত কাজ - ১
এ্যাসাইনমেন্ট বা নির্ধারিত কাজ

(খ) (a) এর বিপরীত ফাংশন সম্ভব কিনা তা যুক্তিসহ উপস্থাপন কর।
(গ) (b) এর ক্ষেত্রে $x\neq 3$ এর জন্য ফাংশনটি এক-এক এবং সার্বিক কিনা তা যুক্তি দিয়ে নিজস্ব মতামত উপস্থাপন কর।
৮ম শ্রেণির ৩য় সাপ্তাহের অ্যাসাইনমেন্ট-এর উচ্চতর গণিত প্রশ্ন দেয়া
হলো :
নমুনা সমাধান
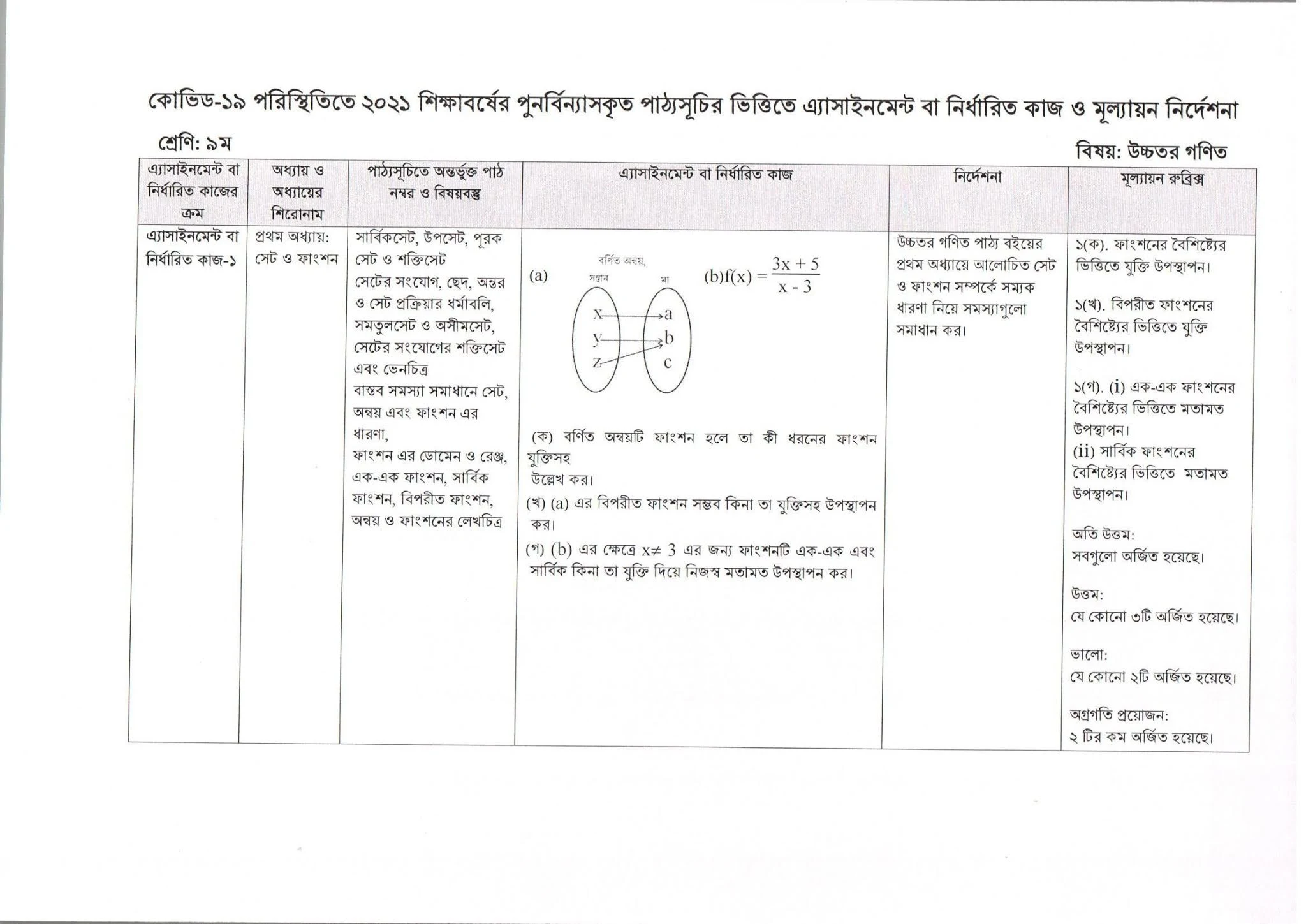
(ক) বর্ণিত অন্বয়টি ফাংশন হলে তা কী ধরনের ফাংশন যুক্তিসহ উল্লেখ
কর।
নমুনা সমাধান :
উক্ত অন্বয়টি একটি ফাংশন।
আমরা জানি, যদি কোন অন্বয় $f:A\rightarrow B$ হয় যেখানে A সেটের
প্রতিটি উপাদান B সেটের যদি এবং কেবল যদি একটি উপাদানের সাথে সম্পর্ক যুক্ত
হয়, তবে সেই অন্বয়কে ফাংশন বলা হবে।
এখানে,
x → a
y → b
z → b
সুতরাং বলা যায়, উক্ত অন্বয়টি একটি ফাংশন।
(খ) (a) এর বিপরীত ফাংশন সম্ভব কিনা তা যুক্তিসহ উপস্থাপন
কর।
নমুনা সমাধান :
ফাংশনটির বিপরীত ফাংশন সম্ভব নয়।
কারণ আমরা জানি, কোনো ফাংশনের বিপরীত ফাংশন তখনই থাকবে যখন ফাংশনটি অবশ্যই এক
- এক ফাংশন এবং সার্বিক ফাংশন হবে।
এখন, এক-এক ফাংশনের শর্ত অনুযায়ী কোন সেটের উপাদানগুলোর কেবলমাত্র অন্য সেটের
একটি উপাদানের প্রতিবিম্ব হবে। কিন্তু y → b এবং z → b যেখানে b দুটি উপাদানের প্রতিবিম্ব।
∴ বলা যায় - ফাংশনটি এক-এক ফাংশন নয়।
আবার, সর্বিক ফাংশন হতে চাইলে সেটের প্রতিটি উপাদানের প্রতিবিম্ব থাকতে হবে।
কিন্তু c উপাদানে কোনো প্রতিবিম্ব আমরা দেখতে পাচ্ছি না।
∴ বলা যায় - ফাংশনটি সার্বিক নয়।
সুতরাং, ফাংশনটির বিপরীত ফাংশন সম্ভব নয়।
(গ) (b) এর ক্ষেত্রে $x\neq 3$ এর জন্য ফাংশনটি এক-এক এবং সার্বিক
কিনা তা যুক্তি দিয়ে নিজস্ব মতামত উপস্থাপন কর।
নমুনা সমাধান :

সুতরাং, ফাংশনটি সার্বিক ফাংশন।
আবার ধরি,
$x_{1}$ এবং $x_{1}$ ; $f(x)$ এর দুটি উপাদান। যেখানে $x_{1}\neq x_{2}$
যদি, $f\left (x_{1} \right )\neq f\left (x_{2} \right )$ হয় কেবল মাত্র তবেই ফাংশনটি এক-এক হবে।
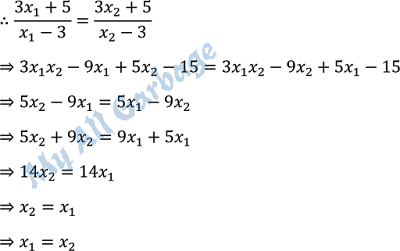
সুতরাং, $f\left (x_{1} \right )\neq f\left (x_{2} \right )$ ফাংশনটি এক-এক নয়।
Azibul Hasan
1st April, 2021
আরো দেখুন :
৪র্থ সপ্তাহের নমুনা সমাধান :
৩য় সপ্তাহের অন্যান্য বিষয়ের নমুনা সমাধান :