দ্বিতীয় অ্যাসাইনমেন্ট
পদার্থ বিজ্ঞান (২য় পত্র)
২য় সপ্তাহ
(ক) এন্ট্রপিস মাধ্যমে তাপগতিবিদ্যার ২য় সূত্র লেখ। তিন প্রক্রিয়ায় [(১) পরিবহন (২) পরিচলন ও (৩) বিকিরণ] তাপের সঞ্চালনের ক্ষেত্রে এন্ট্রপি বৃদ্ধি পায় নাকি হ্রাস পায়? উত্তরের পক্ষে গাণিতিক যুক্তি বিশ্লেষণ করো।
(খ) ধরো তুমি $27^\circ C$ তাপমাত্রায়, স্বাভাবিক চাপের এক গ্রাস হাইড্রোজেন গ্যাসের আয়তন সমোষ্ণ প্রক্রিয়ায় প্রসারিত করে চারগুণ করলে। এতে এন্ট্রপির পরিবর্তন নির্ণয় করো।
(গ) সমোষ্ণ প্রক্রিয়ার প্রসারিত করার ক্ষেত্রে চাপের পরিবর্তন হবে কি না-ব্যাখ্যা করো। হাইড্রোজেন গ্যাসের এই প্রসারণে কৃত কাজের মান নির্ণয় করো।
(ঘ) সমচাপ প্রক্রিয়ায় এক গ্রাম হাইড্রোজেন গ্যাসের আয়তন চার গুণ প্রসারণে এনট্রপির পরিবর্তন হবে কিনা তা নির্ণয় করে দেখাও। সমচাপ ও সমোষ্ণ প্রক্রিয়ায় গ্যাসের এই আয়তন প্রসারণে এন্ট্রপির পরিবর্তনের তুলনা করো।
(ঙ) কার্নোর চক্রকে তাপমাত্র বনাম এন্ট্রপি লেখচিত্রের সাহায্যে অংকন করে িএর বিভিন্ন ধাপ ব্যাখ্যা করো।
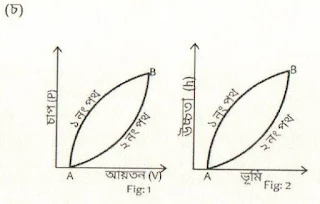 |
Fig: 1 এর ক্ষেত্রে এন্ট্রপির পরিবর্তন এবং Fig: 2 এর ক্ষেত্রে অীভকর্ষ দ্বারা কাজ অবস্থানান্তরের জন্য নির্বাচিত পথের উপর নির্ভর করে কিনা? উত্তরের পক্ষে যুক্তি চিত্রের আলোকে গাণিতিকভাবে ব্যাখ্যা করো।
নির্দেশনা :
পরিমাপের সকল একক S.I ইউনিট হবে।
নমুনা সমাধান
(ক)
প্রথম অংশ :
ক্লাসিয়াসের মতে অপগতিবিদ্যার দ্বিতীয় সূত্র : প্রকৃতির সকল ভৌত অথবা রাসায়নিক ক্রিয়া এমনভাবে সংঘটিত হয় যার ফলে সার্বিক অবস্থার এন্ট্রপি বৃদ্ধি পায়।
অপগতিবিদ্যার ২য় সূত্রকে গাণিতিকভাবে সংজ্ঞায়িত করার জন্য ধরা যাক একটি ব্যবস্থার প্রাথমিক ও চূড়ান্ত অবস্থা $A$ ও $B$ তে এন্ট্রপির মাল $S_A$ ও $S_B$, সুতরাং ব্যবস্থাটির এন্ট্রপির পরিবর্তন,
$S_B-S_A=\int_A^B\frac{dQ}T$
যদি A ও B অবস্থা পরস্পর খুব কাছাকাছি হয়, তাহলে, $ds=\frac{dQ}T$
$\therefore dQ=Tds$
এটি অপগতিবিদ্যার দ্বিতীয় সূত্রের গাণিতিক সংজ্ঞা।
(খ)
দেওয়া আছে,
$\begin{array}{l}T_1=27^\circ C=300K\\V_2=4V_1\\m=1gm\end{array}$
আমরা জানি, সমোষ্ণ প্রক্রিয়ায়,
এন্ট্রপির পরিবর্তন,
$\triangle S=nR\ln\frac{V_2}{V_1}$
$=\frac12\times8.314\times\ln\frac{4V_1}{V_1}$
$=\frac12\times8.314\times\ln4$
$=\frac12\times8.314\times\ln4$
$=5.7628JK^{-1}$ [Answer]
(গ)
চাপের পরিবর্তন হবে,
প্রশ্নমতে, $V_2=4V_1$
আমরা জানি, সমোষ্ণ প্রক্রিয়ায়,
$P_1V_1=P_2V_2$
বা, $\frac{P_1}{P_2}=\frac{V_2}{V_1}$
বা, $\frac{1}{P_2}=\frac{4V_1}{V_1}$ [ $\because$ স্বাভাবিক চাপ, $P_1=1atm$]
বা, $P_2=\frac14$
$\therefore P_2=0.25 atm
$\therefore$ চাপের পরিবর্তন,
$\triangle P=\left(P_1-P_2\right)$
$=\left(1-0.25\right)atm$
$=0.75atm$ [Answer]
২য় অংশ :
সমোষ্ণ প্রক্রিয়ায় কৃতকাজ,
$w=nRT\;\ln\frac{V_2}{V_1}$
$=\frac12\times8.314\times300\times\ln\frac{4V_1}{V_1}$
$=1728.9j$ [Answer]
(ঘ)
আমজা জনি, সমচাপ প্রক্রিয়ায়, এন্ট্রপির পরিবর্তন,
$dS=\frac{dQ}T$
বা, $\int_{S_1}^{S_2}dS=\int_{T_1}^{T_2}\frac{nCpdT}T$
বা, $S_2-S_1=nCp\int_{T_1}^{T_2}\frac1{T_2}dT$
বা, $\triangle S=nCp\left[\ln T\right]_{T_1}^{T_2}$
বা, $\therefore\triangle S=nCp\ln\frac{T_2}{T_1}$
$Cp=\frac{yR}{y-1}$
যেহেতু হাইড্রোজেন গ্যাস দ্বিপরমানুক তাই হাইট্রোজেন গ্যাসের জন্য $y=\frac75$
$\therefore Cp=\frac{{\displaystyle\frac75}R}{{\displaystyle\frac75}-1}=\frac72R$
সমচাপ প্রক্রিয়ায়,
$\frac{V_1}{T_1}=\frac{V_2}{T_2}$
$\therefore\frac{T_2}{T_1}=\frac{V_2}{T_2}$
$\therefore\triangle S=nCp\ln\frac{T_2}{T_1}$
$=n\frac72R\;\ln\frac{V_2}{V_1}$
$=\frac72\times\frac12\times8.314\times\ln\frac{4V_1}{V_1}$
$=20.17JK^{-1}$
সমোষ্ণ প্রক্রিয়ায় এন্ট্রাপির পরিবর্তন, $\triangle S_1=20.17JK^{-1}$
সমচাপ প্রক্রিয়ায় এন্ট্রাপির পরিবর্তন, $\triangle S_2=20.17JK^{-1}$
$\therefore\triangle S_2>\triangle S_1$
বা, $\frac{\triangle S_2}{\triangle S_1}=\frac{20.17}{5.75}=3.5$
$\therefore$ সমচাপ প্রক্রিয়ায় $3.5$ গুণ বেশি এন্ট্রপি পরিবর্তন হয়।
(ঙ)
কার্নো চক্রের তাপমাত্রা $(T)$ বনাম এন্ট্রপি $(6)$ লেখাচিত্র নিচে অংকন করা হলো:
 |
| চিত্র : কর্নো ইঞ্জিন (T~S) গ্রাফ |
ধাপসমূহ নিম্নে বর্ণনা করা হলো :
প্রথম ধাপ (1 থেকে 2) = সমোষ্ণ প্রসারণ :
এই ধাপে তাপমাত্রার পরিবর্তন হয় না। অর্থাৎ তাপমাত্রা ধ্রুব থাকে। 1 বিন্দুতে যে তাপমাত্রা রয়েছে, 2 বিন্দুতেও একই তাপমাত্রা বিরাজ করে। শুধু তাপের পরিবর্তন হয় এ ধাপে $Q_1$ পরিমাণ তাপ শোষিত বা গৃহীত হয়। ফলে এনট্ট্রপি বৃদ্ধি পায়।
দ্বিতীয় ধাপ (2 থেকে 3) = রুদ্ধতাপীয় প্রসারণ :
এই ধাপে তাপমাত্রার পরিবর্তন ঘটে কিন্তু কোনো তাপের পরিবর্তন হয় না। তাপের পরিবর্তন না হওয়ায় এন্ট্রপির কোনো পরিবর্তন হয় না।
তৃতীয় ধাপ (3 থেকে 4) = সমোষ্ণ সংকোচন :
এই অংশে 3 থেকে 4 অবস্থান পর্যন্ত তাপমাত্রার কোনো পরিবর্তন হয় না। কিন্তু তাপ বর্তিত হয় ফলে এন্ট্রপি হ্রাস পায়।
চতুর্থ ধাপ (4 থেকে 1) = রুদ্ধ তাপীয় সংকোচন :
এই ধাপে ও তাপের পরিবন্তন না হওয়ায় এন্ট্রপি অপরিবর্তিত থাকবে।
এটি প্রত্যাগামী প্রক্রিয়া হওয়ায় মোট এন্ট্রপির পরিবর্তন সর্বদা শূন্য হবে।
(চ)
Fig-1 এর ক্ষেত্রে :
ধরি, একটি বস্তু $A$ অবস্থা হতে $B$ অবস্থায় 1নং পথে গিয়ে পুনরায় $B$ অবস্থা হতে ২নং পথ দিয়ে $A$ অবস্থায় ফিরে এলো। সম্পূর্ণ পরিবর্তনের জন্য এন্ট্রপির পরিবর্তন $\int_A^B{\left(ds\right)}_1+\int_B^A{\left(ds\right)}_2$। কিন্তু পথ দুটি দ্বারা একটি প্রত্যাগামী চক্রের সৃষ্টি হয়েছে। এ চত্রের জন্য এন্ট্রপির মোট পরিবর্তন শূন্য।
$\int_A^B{\left(ds\right)}_1+\int_B^A{\left(ds\right)}_2=0$
বা, $\int_A^B{\left(ds\right)}_1=-\int_B^A{\left(ds\right)}_2$
বা, $\int_A^B{\left(ds\right)}_1=\int_A^B{\left(ds\right)}_2$
এই সমীকরণটি থেকে বোঝা যায় যে, $A$ অবস্থা হতে $B$ অবস্থায় 1নং বা, 2নং যে পথই ব্যবহার করা হোক না কেন এন্ট্রপির পরিবর্তন সমান থাকে।
সুতরাং, এন্ট্রপির পরিবর্তন পথ নির্ভরশীল নয়।
Fig-2 এর ক্ষেত্রে,
ধরি, $m$ ভরের একটি বস্তুকে $A$ বিন্দু হতে উপরে B বিন্দুতে নিয়ে যাওয়া হলে এতে অবিকর্ষীয় বলের বিপরীত দিকে সরণ হয় $h$
সেক্ষেত্রে কাজ, $w_1=-mgh$
আবার,
$B$ বিন্দু হতে $A$ বিন্দুতে স্থানান্তর করলে অবিকর্ষ বলের দিকে সরণ $h$
এক্ষেত্রে কৃতকাজ $w_2=mgh$
$\therefore$ মোট কৃত কাজ $=w_1-w_2 = -mgh+mgh=0$
সুতরাং, অবিকর্ষ বল দ্বারা কৃতকাজ আদি ও চূড়ান্ত অবস্থানের উপর নির্ভর করে পথের উপর নয়।
প্রথম অ্যাসাইনমেন্ট
পদার্থ বিজ্ঞান (১ম পত্র)
১ম সপ্তাহ
(ক) $P$ বিন্দুটির অবস্থান ভেক্টর নির্ণয় করো। $\overrightarrow{PQ}$ এর
সমান্তরালে একটি একক ভেক্টর নির্ণয় করো।
(খ) $\overrightarrow P$ ও $\overrightarrow Q$ ভেক্টরদ্বয় একটি ত্রিভুজের দুটি
সন্নিহিত বাহু নির্দেশ করলে, ত্রিভুজের ক্ষেত্রফল কত?
(গ) ধরো তোমার প্রসঙ্গ কাঠামোতে অপর একটি ভেক্টর $\overrightarrow R=\widehat
i+2\widehat j-3\widehat k$। $\overrightarrow P$, $\overrightarrow Q$ এবং
$\overrightarrow R$ চিত্র ১ এর ন্যায় একটি ঘন সামান্তরিকের তিনটি বাহু নির্দেশ
করলে সামান্তরিকটির আয়তন নির্ণয় করো ও উত্তরের পক্ষে তোমার ব্যাখ্যা উপস্থাপন
করো।

|
| চিত্র ১ : ঘন সামান্তিরিক |
(ঘ) এবার একটি নদীর প্রস্থ হিসেবে $\overrightarrow P$ এর মানকে বিবেচনা করো। ধরো, $\overrightarrow Q$ সেই নদীর স্রোহের বেগ ও $\overrightarrow R$ নৌকার বেগ নির্দেশ করছে এবং তুমি ঐ নৌকায় বসে আছ। এখন সবচেয়ে কম সময়ে নদী পার হতে তুমি কী ব্যবস্থা করবে? গাণিতিকভাবে দেখাও। (নৌকাটি এর চেয়ে জোরে চালানো সম্ভব নয়)
(ঙ) নদী পার হওয়ার সবচেয়ে কম সময় কত ছিল তা নির্ণয় করো।
(চ) এখন এই নদী সবচেয়ে কম দূরত্বে পার হতে নৌকাটির বেগের ও সময়ের কোনো পরিবর্তন
করতে হবে কিনা? গাণিতিক যুক্তি বিশ্লেষণ করো।
নির্দেশনা :
পরিমাপের ক্ষেত্রে দৈর্ঘ্য কিলোমিটার এককে এবং বেগ কিলোমিটার/ঘণ্টা এককে পরিমাপ
করতে হবে।
নমুনা সমাধান
(ক)
P এর অবস্থান ভেক্টর,
$\overrightarrow{OP}=\overrightarrow P=3\widehat i-4\widehat j+5\widehat k$
Q এর অবস্থান ভেক্টর,
$OQ=\overrightarrow Q=2\widehat i-\widehat j+\widehat k$
$\overrightarrow{OQ}=\overrightarrow Q-\overrightarrow P$
$=2\widehat i-\widehat j+\widehat k-3\widehat i+4\widehat j-5\widehat k$
$=-\widehat i+3\widehat j-4\widehat k$
$\therefore\left|\overrightarrow{PQ}\right|=\sqrt{\left(-1\right)^2+3^2+\left(-4\right)^2}$
$=\sqrt{1+9+16}$
$=\sqrt{26}$
$\therefore\overrightarrow{PQ}$ এর সমান্তরালে একক ভেক্টর
$=\frac{\overrightarrow{PQ}}{\left|\overrightarrow{PQ}\right|}$
$=\frac{-\widehat i+3\widehat j-4\widehat k}{\sqrt{26}}$
$=-\frac{1}{\sqrt{26}}\widehat i+\frac3{\sqrt{26}}\widehat
j-\frac4{\sqrt{26}}\widehat k$ [Answer]
(খ)
‘ক’ থেকে প্রাপ্ত
$\overrightarrow P=3\widehat i-4\widehat j+5\widehat k$
$\overrightarrow Q=\widehat i-\widehat j+\widehat k$
$\overrightarrow P$ ও $\overrightarrow Q$ ত্রিভুজের সন্নিহিত বাহু নির্দেশ
করলে,
আমরা জানি,
ক্ষেত্রফল $=\frac12\left|\overrightarrow P\times\overrightarrow Q\right|$
তাহলে $\overrightarrow P\times\overrightarrow Q=\begin{bmatrix}\widehat
i&\widehat j&\widehat k\\3&-4&5\\2&-1&1\end{bmatrix}$
$=\widehat i\left(-4+5\right)-\widehat j\left(3-10\right)+\widehat
k\left(-3+8\right)$
$=\widehat i+7\widehat j+5\widehat k$
$\therefore\left|\overrightarrow P\times\overrightarrow Q\right|$
$=\sqrt{1^2+7^2+5^2}$
$=\sqrt{1+49+25}$
$=\sqrt{75}$
$\therefore$ ত্রিভুজের ক্ষেত্রফল
$=\frac12\left|\overrightarrow P\times\overrightarrow Q\right|$
$=\frac12\times\sqrt{75}$
$=\frac{\sqrt{75}}{2}$ বর্গ একক [Answer]
(গ)
দেওয়া আছে,
$\begin{array}{l}\overrightarrow P=3\widehat i-4\widehat j+5\widehat
k\\\overrightarrow Q=2\widehat i-\widehat j+\widehat k\\\overrightarrow
R=\widehat i+2\widehat j-3\widehat k\end{array}$
চিত্রনানুযায়ী, ভূমির ক্ষেত্রফল $=\left|\overrightarrow P\times\overrightarrow
Q\right|=PQ\sin\theta$
এবং
সামান্তরিকের আয়তন = ভূমির ক্ষেত্রফল $\times$ উচ্চতা $=\overrightarrow
P\times\overrightarrow Q.\overrightarrow R$
$\therefore\overrightarrow P\times\overrightarrow Q=\begin{bmatrix}\widehat
i&\widehat j&\widehat k\\3&-4&5\\2&-1&1\end{bmatrix}$
$=\widehat i+7\widehat j+5\widehat k$ [‘খ’ হতে প্রাপ্ত]
$\therefore\left(\overrightarrow P\times\overrightarrow
Q\right).\overrightarrow R=\left(\widehat i+7\widehat j+5\widehat
k\right).\left(\widehat i+2\widehat j-3\widehat k\right)$
$=1+14-15$
$=0$ ঘন একক।
যেহেতু, এদের আয়তন শূন্য, সেহেতু এরা সমতলীয়।
$\therefore$ $\overrightarrow P$, $\overrightarrow Q$ ও $\overrightarrow R$
ভেক্টর সমতলীয়।
(ঘ)
নদীর প্রস্থ, $\left|\overrightarrow
P\right|=\sqrt{3^2+\left(-4\right)^2+5^2}=\sqrt{50}$ কি.মি.
স্রোতের বেগ, $\left|\overrightarrow
Q\right|=\sqrt{2^2+\left(-1\right)^2+1^2}=\sqrt{6}$ কি.মি./ঘণ্টা
নৌকার বেগ, $\left|\overrightarrow
R\right|=\sqrt{1^2+2^2+\left(-3\right)^2}=\sqrt{14}$ কি.মি./ঘণ্টা
ধরি, স্রোতের বেগ, $V_r=\sqrt{6}$ কি.মি./ঘণ্টা এবং নৌকার বেগ, $V_b=\sqrt{14}$
কি.মি./ঘণ্টা।
ধরি, নৌকাটি পৌঁছানোর সর্বনিম্ন সময়, $t$ এবং নৌকাটি স্রোতের সাথে $\alpha$ কোনে
যাত্রা করে।
$\therefore$ নৌকার বেগ ও স্রোহের বেগের উৎপাংশের যোগফল,
$\begin{array}{l}=V_b\sin\alpha+V_r\sin0^\circ\\=V_b\sin\alpha\end{array}$
তাহলে নদী পার হতে সর্ব নিম্ন সময়, $t=\frac d{V_b\sin\alpha}$
$t$ সর্বনিম্ন হবে যদি $\sin\alpha=1$ বা $\alpha90^\circ$ হয়।
(ঙ)
$\therefore t=\frac
d{V_b\sin90^\circ}=\frac{\sqrt{50}}{\sqrt{14}\times1}=1.89$ ঘণ্টা।
তাহলে নদী পার হওয়ার সবচেয়ে কম সময় ছিল $1.89$ ঘণ্টা।
(চ)
ধরি, লব্ধি বেগ, $w$
$\therefore w=\sqrt{R^2+Q^2}$
$=\therefore w=\sqrt{\left(\sqrt{14}\right)^2+\left(\sqrt6\right)^2}$
$=\sqrt{14-6}$
$=\sqrt{6}$ কি.মি./ঘণ্টা
আমরা জানি,
সময়, $t=$
নদীর প্রস্থ
⁄
উলম্ব বরাবর নৌকার বেগের উপাংশ
$=\frac Pw=\frac{\sqrt{50}}{\sqrt8}=2.5$ ঘণ্টা।সবচেয়ে কম দূরত্বে পার হতে গেলে সময় বেশি লাগে $=2.5-1.89$ ঘণ্টা $=0.61$ ঘণ্টা।
আবার, $t=\frac P{R\sin\alpha}$ অর্থাৎ, $t\alpha\frac1R$
যেখানে, $R=$ নৌকার বেগ
সুতরাং, নৌকার বেগ বাড়ালে নূন্যতম দূরত্বে অতিক্রম করা যায়।



