সেট
(Set)
সেট শব্দটি আমাদের কাছে অনেক পরিচিত একটি শব্দ। বাস্তব সংখ্যার সেট, স্বাভাবিক
সংখ্যার সেট, মূলদ সংখ্যার সেট ইত্যাদি। আধুনিক হাতিয়ার হিসেবে সেটের ব্যবহার
ব্যাপক। জার্মান গণিতবিদ জর্জ ক্যান্টর (১৮৪৫-১৯১৮) সেট সম্পর্কে সর্বপ্রথম ধারণা
ব্যাখ্যা করেন। তিনি অসীম সেটের ধারণা প্রদান করে গণিত শাস্ত্রে আলোড়ন সৃষ্টি
করেন এবং তাঁর সেটের ধারণা “সেট তত্ত্ব” নামে পরিচিত।
সেট (Set) :
বাস্তব বা চিন্তা জগতের সুসংজ্ঞায়িত বস্তুর সমাবেশকে সেট (Set) বলে। যেমন:
2, 3, 4 সংখ্যা তিনটির সেট A = {2, 3, 4}
১. সেটকে সাধারণত ইংরেজি বর্ণমালার বড় হাতের অক্ষর A, B, C,........ X, Y, Z
ইত্যাদি দ্বারা প্রকাশ করা হয়।
২. সেটের প্রত্যেক বস্তু বা সদস্যকে সেটের উপাদান (element) বলা হয়। যেমন:
উপরোক্ত A সেটের উপাদান বা element হচ্ছে 2, 3, 4
৩. সেটের উপাদান বা element প্রকাশের চিহ্ন $\in$ যাকে পড়া হয় belongs to. যেমন :
B={a,b} সুতরাং a $\in$ B এবং b $\in$ B
এখানে a belongs to B এবং b belongs to B. সেট B তে c নামের কোনো উপাদান
(element) নেই, সুতরাং c $\not\in$ B অর্থাৎ c, B এর element নয় (c doesn't
belong to B)।
সেট প্রকাশের পদ্ধতি :
সেটকে ২ পদ্ধতিতে প্রকাশ করা যায়। যথা: তালিকা পদ্ধতি (Roster Method or, Tabular
Method) এবং সেট গঠন পদ্ধতি (Set Builder Method)।
(ক) তালিকা পদ্ধতি (Roster Method or, Tabular Method) : এ পদ্ধতিতে সেটের
সকল উপাদান সুনির্দিষ্টভাবে উল্লেখ করে দ্বিতীয় বন্ধনী { } এর মধ্যে আবদ্ধ করা হয়
এবং একাধিক উপাদান থাকলে 'কমা' ব্যবহার করে উপাদানগুলোকে আলাদা করা হয়। যেমন:
A = {a, b}
B = {2, 4, 6, 8}
(খ) সেট গঠন পদ্ধতি (Set Builder Method) : এ পদ্ধতিতে সেটের উপাদান
সুনির্দিষ্টভাবে উল্লেখ না করে উপাদান নির্ধারণের জন্য সাধারণ ধর্মের উল্লেখ
থাকে। যেমন :
A = { x : x স্বাভাবিক বিজোড় সংখ্যা }
B = { x : x জোড় স্বাভাবিক সংখ্যা }
নোট — ' : ' একে সংক্ষেপে 'যেন' আর ইংরেজিতে such that বলে। এখানে x such that x
এভাবে বলা হয়। সেট গঠন পদ্ধতি কে অনেকে Rule Method পদ্ধতি বলে থাকে।
সসীম সেট (Finite Set) :
যে সেটের উপাদান সংখ্যা বা element গণনা করে নির্ধারণ করা যায়, তাকে সসীম সেট
(Finite Set) বলে। যেমন:
D = { x, y, z}
E = { 3, 6, 9,............, 60}
এখানে D সেটে ৩ টি এবং E সেটে ২০ টি উপাদান / element আছে।
অসীম সেট (Infinite Set) :
যে সেটের উপাদান সংখ্যা বা element গণনা করে শেষ করা যায় না, তাকে অসীম সেট
(Infinite Set) বলে। যেমন:
A = { x : x বিজোড় স্বাভাবিক সংখ্যা }
N = { 1, 2, 3, 4, 5,.......... }
ফাঁকা সেট (Empty Set) :
যে সেটের কোনো উপাদান নেই তাকে ফাঁকা সেট বা Empty Set বলে। ফাঁকা সেট (Empty
Set) কে $\varnothing$ চিহ্ন অথবা ফাঁকা { } দ্বারা প্রকাশ করা হয়। যেমন:
{x $\in$ N : 10<x<11} অথবা, {x $\in$ N : Prime Number এবং 23<x<29}
উপসেট (Subset) :
যদি A সেটের প্রত্যেক উপাদান B এরও উপাদান হয়, তবে A কে B এর উপসেট বা Subset
বলে।
যেমন : A = { a, b } একটি সেট। এখন এই সেটের উপাদান থেকে { a, b }, { a }, { b }
সেটগুলো গঠন করা যায়। আবার, কোনো উপাদান না নিয়ে $\varnothing$ বা { } সেট
গঠন করা যায়। সুতরাং, এখানে A সেটের উপসেটগুলো হচ্ছে { a, b }, { a }, { b }, {
}।
উপসেটকে যেভাবে লিখতে হবে : $\subseteq$ অর্থাৎ $B \subseteq A$
ধরি, P = { 1, 2, 3 }, Q = { 2, 3 }, R = {1, 3 } তাহলে P, Q, R প্রত্যেকে P এর
উপসেট। অর্থাৎ, $P \subseteq P$, $Q \subseteq P$ এবং $R \subseteq P$
Note: $\varnothing$ অথবা { } যেকোনো সেটের উপসেট।
প্রকৃত উপসেট (Proper Subset) :
কোনো সেট থেকে গঠিত উপসেটের মধ্যে যে উপসেটগুলোর উপাদান সংখ্যা প্রদত্ত সেটের
উপাদান সংখ্যা অপেক্ষা কম এদেরকে প্রকৃত উপসেট বা Proper Subset বলে।
যেমন:
A = { 3, 4, 5, 6 } এবং B = { 3, 5 } দুইটি সেট।
উল্লেখ্য, এখানে B সেটের প্রত্যেকটি উপাদান A সেটের ভিতর আছে এবং B সেটের উপাদান
সংখ্যা A সেটের উপাদান থেকে কম। সুতরাং B সেট হল A সেটের প্রকৃত উপসেট
(Proper Subset) বলে।
প্রকৃত উপসেট (Proper Subset) যেভাবে প্রকাশ করা হয়: প্রকৃত উপসেট (Proper
Subset) কে $\subset$ চিহ্ন দিয়ে লেখা হয়।
ধরি, A = { 3, 4, 5, 6 } এবং B = { 3, 5 } অর্থাৎ, B $\subset$ A (B is a
proper subset of A)
নোট: কোন সেটের উপাদান সংখ্যা n হলে ঐ সেটের উপসেটের সংখ্যা $2^n$ এবং
প্রকৃত উপসেটের সংখ্যা $2^n-1$)
সেটের সমতা (Equivalent Set) :
দুইটি সেটের উপাদান একই হলে তাদের সমান সেট (Equivalent Set) বলে। যেমন:
A = { 3, 5, 7, 8 } এবং
B = { 5, 3, 3, 8, 7 } হলো দুটি সমান সেট বা (Equivalent Set)।
খেয়াল করবেন : A = B যদি এবং কেবল যদি $B \subseteq A$ এবং $A \subseteq
B$ হয়।
মনে রাখুন : কোনো সেটের উপাদানগুলোর সিরিয়াল বদলালে বা কোনো উপাদানের
পুনরাবৃত্তি করলে সেটের কোনো পরিবর্তন হয়না।
সেটের অন্তর (Difference of Sets) :
ধরুন,
A = { 1, 2, 3, 4, 5 } এবং
B = { 3, 5 }
এখন A সেট থেকে B সেটের উপাদানগুলো বাদ দিলে যে সেটটি হয় তা হচ্ছে { 1, 2, 4 }
এবং একে লেখা হয় A \ B অথবা A - B এবং একে পড়ার সময় বলতে হয় A বাদ B।
সুতরাং,
A \ B অথবা A - B = {1, 2, 3, 4, 5} - {3, 5} = { 1, 2, 4 }
সার্বিক সেট (Universal Set) :
সংশ্লিষ্ট সকল সেট যদি একটি নির্দিষ্ট সেটের উপসেট হয় তবে ঐ নির্দিষ্ট সেটকে তার
উপসেটগুলোর সার্বিক সেট (Universal Set) বলে।
১. সার্বিক সেট (Universal Set) কে সাধারণত U দ্বারা প্রকাশ করা হয়।
২. তবে অন্য কোনো প্রতীকের সাহায্যে সার্বিক সেট বা Universal Set কে প্রকাশ করা
যায়।
যেমন: C = { 2, 4, 6,..............., } এবং N = { 1, 2, 3, 4, 5, 6,
7,........................., } হলে C সেটের সাপেক্ষে N হচ্ছে সার্বিক সেট।
পূরক সেট (Complement of a Set) :
যদি A, B দুইটি সেট হয় এবং A সেটের যেসব উপাদান B এর উপাদান নয়, ঐ উপাদানগুলোর
সেটকে A সেটের পরিপ্রক্ষিতে B সেটের পূরক সেট বা Complement of a Set বলে।

পূরক সেট (Complement of a Set) যেভাবে লেখা হয় : A এর পূরক সেটকে $A^c$
অথবা $A'$ এবং গাণিতিকভাবে A \ B বা A - B তে লেখা হয়।
সংযোগ সেট (Unions of Sets) :
দুই বা ততোধিক সেটের সকল উপাদান নিয়ে গঠিত নতুন সেটকে সংযোগ সেট বা Unions of
Sets বলে। মনে করি, A এবং B দুইটি সেট। এখন A ও B সেটের সংযোগ সেটকে A U B
দ্বারা প্রকাশ করা হয় এবং একে পড়া হয় A Union B।
যেমন:
A = { 3, 4, 5 } এবং B = { 4, 6, 8 }
সুতরাং A $\cup$ B = {3, 4, 5} $\cup$ {4, 6, 8} = {3, 4, 5, 6, 8}
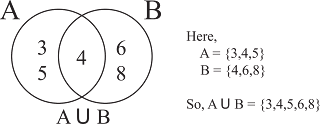
ছেদ সেট (Intersection of Sets) :
দুই বা ততোধিক সেটের সকল উপাদান থেকে সাধারণ বা কমন উপাদান নিয়ে গঠিত নতুন সেটকে
ছেদ সেট বা Intersection of Sets বলে। মনে করি, A এবং B দুইটি সেট। এখন A ও
B সেটের ছেদ সেটকে A $\cap$ B দ্বারা প্রকাশ করা হয় এবং একে পড়া হয় A
intersection B।
যেমন:
A = { 3, 4, 5, 8} এবং B = { 4, 6, 8 }
সুতরাং A $\cap$ B = {3, 4, 5, 8} $\cap$ {4, 6, 8} = { 4, 8 }

নিশ্ছেদ সেট (Disjoint Set) :
দুইটি সেটের মধ্যে যদি কোনো সাধারণ বা কমন উপাদান না থাকে তবে সেট দুইটিকে পরস্পর
নিশ্ছেদ সেট বা Disjoint Set বলে। মনে করি, A এবং B দুটি সেট।
A = {1, 2, 3, 4} এবং B = {5, 6, 7, 8}
A $\cap$ B = {1, 2, 3, 4} $\cap$ {5, 6, 7, 8} = $\varnothing$
শক্তি সেট (Power Set) :
মনে করি, A একটি সেট। A সেটের যতগুলো উপসেট হয়, তাদের সেটকে A সেটের শক্তি সেট বা
Power Set বলে এবং একে লেখা হয় P(A)।
যেমন: A = {m, n}; সুতরাং, A সেটের উপসেট হচ্ছে {m, n}, {m}, {n}, { }
শর্ট নোট: কোনো সেটের উপাদান সংখ্যা n হলে তার পাওয়ার সেট বা শক্তি সেটের
উপাদান হচ্ছে $2^n$
দ্যা মরগ্যানের সূত্র (De Morgans Law) : সার্বিক সেট U এর যেকোনো উপসেট A
ও B হলে—
- $\left(A\cup B\right)'=A'\cap B'$
- $\left(A\cap B\right)'=A'\cup B'$
এই প্রতিজ্ঞাকে দ্যা মরগ্যানের সূত্র (De Morgans Law) নামে অভিহিত করা হয়।


