কোণ
(Angle)
জ্যামিতিতে ভাল করতে হলে জ্যামিতির মৌলিক বিষয়বস্তুর উপর খুব ভালোভাবে ধারণা
থাকতে হবে। কোণ বা Angle তেমনিভাবে জ্যামিতির অত্যন্ত গুরুত্বপূর্ণ ও মৌলিক একটি
বিষয়। কোণ অংকন করা, চিহ্নিত করা এবং কোণের বর্ণনা ও এদের সঠিক ব্যবহার না জানলে
জ্যামিতিতে কোণের উপর ভাল আয়ত্ত্ব রাখতে পারবেন না। আমরা আজকে কোণ কি, এর
পরিপূর্ণ সংজ্ঞা, কোণের বৈশিষ্ট্য এবং কোণের বিভিন্ন প্রকারভেদ নিয়ে আলোচনা করব
ইনশাআল্লাহ এবং আপনি যদি মনোযোগ সহকারে পুরো কন্টেন্টটি পড়েন তবে কোণ নিয়ে আপনার
আর কোনো কনফিউশান থাকবে না আশা করা যায়৷
সাধারণ অর্থে কোণ বলতে কোণা (গ্রাম্য ভাষায় যাকে কানাকানি) বুঝায়। যেমন: টেবিলের
কোণা, ঘরের কোণা, ছাদের কোণা ইত্যাদি। খেয়াল করলে দেখবেন এই কোণা যেখানে উৎপন্ন
হয় সেটি মূলত ২ টি বাহু মিলনস্থল। সুতরাং, দুটি বাহু কোনো একটি জায়গা বা বিন্দুতে
মিলিত হলল তাকে কোণা বা কোণ বলে।
কোণের ইংরেজি শব্দ Angle যার বাংলা আভিধানিক অর্থ দাঁড়ায় কোণ। কোণ সম্পর্কে
ভালোভাবে জানতে হলে আপনার রেখা, রশ্মি কিংবা রেখাংশ সম্পর্কে ভালো ধারণা থাকতে
হবে। এজন্য আমাদের রেখা, রেখাংশ ও রশ্মি সম্পর্কিত আর্টিকেলটি পড়ুন : রেখা (Line)
কোণের সংজ্ঞা :
দুইটি সরলরেখাংশ/রশ্মি এর প্রান্ত বিন্দুদ্বয় পরস্পর সাথে কোনো বিন্দুতে মিলিত
হয়, বা কোনো সরল রেখা পরষ্পরকে কোনো বিন্দুতে ছেদ করে, তবে ঐ বিন্দুতে কোণ উৎপন্ন
হয়৷
কোণ নির্দেশক চিহ্ন : কোণকে $\angle$ এই চিহ্নের সাহায্যে প্রকাশ করা হয়।
যেমন:

|
| চিত্রে ABC একটি কোণ। $\therefore\angle ABC=\theta$ |
কোণের ব্যবহার :
আমাদের দৈনন্দিন জীবনে কোণের ব্যবহার ব্যাপক। হয়তো আমরা কখনো বুঝতে পারি আবার
কখনো বুঝতে পারি না। পরিমাপে কোণের ব্যবহার ব্যাপক। পরিমিতে কোনো একটি বস্তুর
আয়তন নির্ণয়ে কিংবা ত্রিকোণমিতিতে কোনো বস্তুর দৈর্ঘ্য পরিমাপ করতে কোণের ব্যবহার
বহুল। আমাদের ব্যবহার বিভিন্ন জিনিসপত্র কিংবা নকশা/ডিজাইন করতে কোণের প্রচুর
ব্যবহার হয়। আমাদের আশেপাশে কোণের ব্যবহার সবখানে সবদিকে ছড়িয়ে ছিটিয়ে আছে।
আমাদের দেখা ক্রিকেট খেলায় ৪৫° কোণে ছক্কা মারলে বড় ছক্কা হওয়া কিংবা ফুটবলে গোল
করতে কোণের সূক্ষ্ম ব্যবহার করেন ট্রাইকাররা। আর তাই কোণের ব্যবহার লিখিয়ে বুঝানো
সম্ভব নয়। কারণ, আমাদের এই সুন্দর পৃথিবীতে সবখানে কোণের উপস্থিতি ও ব্যবহার
বিদ্যমান।
কোণের কিছু বৈশিষ্ট্য নিম্নে দেখানো হল:
১. একটি কোণ তৈরি করতে কমপক্ষে ২ টি রশ্মির দরকার হয়।
২. একটি কোণে একটিমাত্র শীর্ষবিন্দু থাকে।
৩. একটি কোণ কখনোই ৩৬০° থেকে বড় হতে পারবে না।
৪. একটি কোণের দুই বাহুকে আপনি ইচ্ছেমত যতখুশি বড় বা ছোট করুন না কেন, কোণের
পরিমাপ অপরিবর্তিত থাকবে।
৫. আপনি যদি কোণের পরিমাপ পরিবর্তন করতে চান তবে আপনাকে এর ২ বাহুর মধ্যকার
দূরত্বের পার্থক্য পরিবর্তন করতে হবে।
৬. একটি ত্রিভুজের ৩ কোণের সমষ্টি ১৮০° এবং চতুর্ভূজের ৪ কোণের সমষ্টি
৩৬০°।
৭. একটি বৃত্তের কেন্দ্রে উৎপন্ন কোণের পরিমাপ ৩৬০° হয়।
৮. সমবাহু ত্রিভুজের কোণগুলো পরস্পর সমান হয়।
৯. কোণের বাহু দুটির মিলিত বিন্দুর নাম কোণের শীর্ষ বিন্দু।
১০. সমদ্বিবাহু ত্রিভুজে ২ টি সমান কোণ থাকে।
কোণের প্রকারভেদ :
কোণের প্রকারভেদ আসলে এককথায় হয় না। তবে কোণকে বিভিন্ন দৃষ্টিকোণ থেকে কয়েকটি
ভাগে ভাগ করা যায়। যে সকল বিষয়ের উপর ভিত্তি করে কোণকে ভাগ করা যায় নিম্নে সেসকল
বিষয় তুলে ধরা হলো—
ক. সমকোণের ভিত্তিতে
খ. সমান্তরাল সরলরেখার ভিত্তিতে
গ. আলোকরশ্মির উপর ভিত্তি করে
ঘ. সামষ্টিক মানের ভিত্তিতে
ঙ. ক্ষেত্রে অবস্থানের উপর ডিপেন্ড করে
চ. অন্যান্য প্রকারভেদ
নিম্নে এগুলোর বিশদ আলোচনা করা হয়েছে। ভালোভাবে পড়ে নিন৷ আশাকরি, কোনো কনফিউশান
থাকবে না।
ক. সমকোণের ভিত্তিতে : সমকোণের ভিত্তিতে কোণকে সাধারণত ৪ ভাগে ভাগ করা
যায়। যথা—
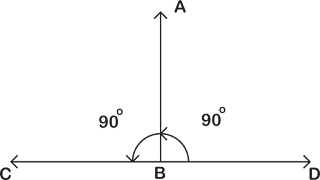
১. সমকোণ : যে কোণের পরিমাপ ৯০° তাকে সমকোণ বলে। অতএব, ৯০° পরিমাণ কোণকে
মূলত সমকোণ বলে।
অথবা, একই রেখার উপর অবস্থিত ২ টি সন্নিহিত কোণ পরস্পর সমান হয়, তাহলে কোণ দুইটির
প্রত্যেকটি এক একটি সমকোণ। সমকোণের বাহু ২ টি পরস্পরের উপর লম্ব থাকে এবং ১ সমকোণ
= ৯০° হয়।
|
|
চিত্রে : $AB\perp CD$ এবং $\angle ABC=\angle ABD=$ এক সমকোণ |
নোট : ডিগ্রির সাহায্যে কোণকে সংজ্ঞায়িত করলে ডিগ্রি সম্পর্কে আপনার পূর্ণ জ্ঞান
থাকা আবশ্যক। যদি বলি ডিগ্রি কি? অনেকে অনেকভাবে একে ডিফাইন করবেন। পরস্পর
লম্বভাবে পতিত দুটি রশ্মির প্রান্তবিন্দু একই হলে রশ্মি দুটি তাদের সাধারণ
প্রান্তবিন্দুতে যে কোণে আনত হয়, তার এক্সাক্ট পরিমাপ ৯০°। এখন যদি এই কোণকে সমান
৯০ টি ভাগে ভাগ করা যায় তবে প্রতিটি ভাগ ১° করে হবে। আর এভাবেই চাঁদা তৈরি করে
তাতে কোণ আঁকা হয়েছে।
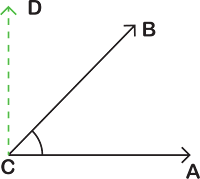
২. সূক্ষ্মকোণ : এক সমকোণ অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে। অর্থাৎ, যে
কোণের পরিমাপ ৯০° অপেক্ষা ছোট তাকে সূক্ষ্মকোণ বলে।
|
| চিত্রে $\angle ACB$ সূক্ষ্মকোণ |
৩. স্থুলকোণ : এক সমকোণ অপেক্ষা বড় কিন্তু ২ সমকোণ অপেক্ষা ছোট কোণকে
স্থুলকোণ বলে। অর্থাৎ, ৯০° অপেক্ষা বড় এবং ১৮০° অপেক্ষা ছোট কোণকে স্থুলকোণ
বলে।

|
|
|
৪. সরলকোণ : দুইটি পরস্পর বিপরীত রশ্মি তাদের সাধারণ প্রান্ত বিন্দুতে যে
কোণ উৎপন্ন করে, তাকে সরল কোণ বলে। অন্যকথায়, যদি কোনো কোণের পরিমাপ ১৮০° হয়, তবে
তাকে সরলকোণ বলে।

|
| চিত্রে $\angle ACD$ সরলকোণ = $180^\circ$ |
খ. সমান্তরাল সরলরেখার ভিত্তিতে : দুই বা ততোধিক সরলরেখা অপর কোনো
সরলরেখাকে ছেদ করলে যে সকল কোণ উৎপন্ন হয়, তার উপর ভিত্তি করে কোণকে ২ ভাগে ভাগ
করা যায়। যথা—
১. একান্তর কোণ : দুটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা তির্যকভাবে
ছেদ করলে ছেদরেখার বিপরীত পার্শ্বে সমান্তরাল রেখা যে কোণ উৎপন্ন করে, তাকে
একান্তর কোণ বলে। একান্তর কোণদ্বয় পরস্পর সমান হয়।

|
|
চিত্রে $AB\parallel CD$ এবং $PS$ তাদের ছেদক। এবং $\angle AQR=\angle DRQ=$ একান্তর কোণ |
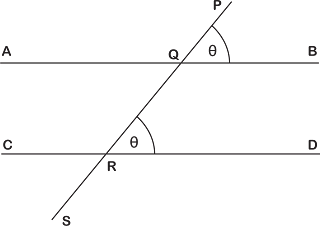
২. অনুরূপ কোণ : দুইটি সমান্তরাল সরলরেখাকে অপর একটি সরলরেখা তির্যকভাবে
ছেদ করলে ছেদকরেখার একই দিকে সমান্তরাল রেখাদ্বয়ের অনুরূপ পার্শ্বে যে কোণ উৎপন্ন
হয়, তাকে অনুরূপ কোণ বলে। অনুরূপ কোণদ্বয় পরস্পর সমান হয়।
|
|
চিত্রে $AB\parallel CD$ এবং $PS$ তাদের ছেদক। এবং $\angle PQB=\angle QRD=$ অনুরূপ কোণ |
গ. আলোকরশ্মির উপর ভিত্তি করে : আলোকরশ্মির উপর ভিত্তি করে কোণকে কয়েকটি
ভাগে ভাগ করা যায়। যথা—
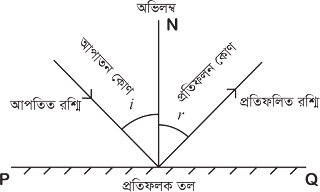
১. আপতন কোণ : আপতিত রশ্মি অভিলম্বের সাথে যে কোণ তৈরি করে, তাকে আপতন কোণ
বলে।
|
| চিত্র : আপতন কোণ |
আপতন কোণকে
i
দ্বারা প্রকাশ করা হয়।
২. প্রতিফলন কোণ : প্রতিফলিত রশ্মি অভিলম্বের সাথে যে কোণ তৈরি করে, তাকে
প্রতিফলন কোণ বলে।
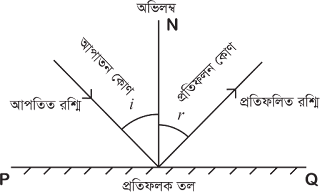
|
| চিত্র : প্রতিফলন কোণ |
প্রতিফলন কোণকে
r
দ্বারা প্রকাশ করা হয়।
৩. প্রতিসরণ কোণ : প্রতিসরিত রশ্মি অভিলম্বের সাথে যে কোণ তৈরি করে, তাকে
প্রতিসরণ কোণ বলে।

|
| প্রতিসরণ কোণ |
৪. ক্রান্তি কোণ : নির্দিষ্ট বর্ণের কোনো আলোক রশ্মি ঘন মাধ্যম থেকে হালকা
মাধ্যমে যাওয়ার সময় আপতন কোণের যে মানের জন্যে প্রতিরসরণ কোণ ৯০° হয়, আপতন কোণের
সেই মানকে ক্রান্তি বা সংকট কোণ বলে। ক্রান্তি কোণের অপর নাম সংকট কোণ। মূলত সংকট
কোণ ও ক্রান্তি কোণ একই জিনিস।
 |
| ক্রান্তি কোণ |
ঘ. সামষ্টিক মানের ভিত্তিতে : দুটি কোণ পাশাপাশি অবস্থান করলে তাদের
অবস্থানের উপর ভিত্তি করে কোণকে ৩ টি ভাগে ভাগ করা যায়। যথা—
১. সন্নিহিত কোণ : দুইটি কোণের যদি একটি সাধারণ বাহু থাকে, তাহলে তাদের
একটিকে অপরটির সন্নিহিত কোণ বলে। অন্যভাবে বললে, দুটি কোণের শীর্ষবিন্দু একই
ধরনের হলে সাধারণ বাহুর উভয় পার্শ্বের কোণ দুটিকে সন্নিহিত কোণ বলে। অর্থাৎ,
পাশাপাশি লেগে থাকা দুইটি কোণকেই সন্নিহিত কোণ বলে।
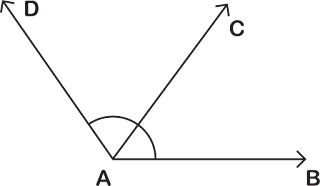
|
| সন্নিহিত কোণ |
২. পূরক কোণ : দুইটি কোণের পরিমাপের যোগফল যদি ৯০° হয়, তাহলে কোণ দুটিকে
একে অপরের পূরক কোণ বলে।

|
| পূরক কোণ |
৩. সম্পূরক কোণ : দুইটি কোণের পরিমাপের যোগফল যদি ১৮০° হয়, তাহলে কোণ
দুটিকে একে অপরের সম্পূরক কোণ বলে।

|
| সম্পূরক কোণ |
ঙ. ক্ষেত্রে অবস্থানের উপর ডিপেন্ড করে : ক্ষেত্রে অবস্থানগত দিকের উপর
ডিপেন্ড করে অর্থাৎ কোনো একটি ক্ষেত্রের বাহিরে ও ভিতরে অবস্থানের উপর ভিত্তি করে
কোণকে ৩ টি ভাগে ভাগ করা যায়। যথা—
১. অন্তঃস্থ কোণ : যে কোন চতুর্ভূজ, বহুভূজ বা ত্রিভুজের ভেতরে বা
অভ্যন্তরে যে কোণ উৎপন্ন হয়, তাকেই অন্তঃস্থ কোণ বলে।
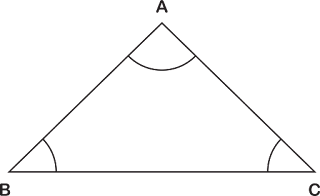
|
| অন্তঃস্থ কোণ |
২. বহিঃস্থ কোণ : কোনো ক্ষেত্র কিংবা চতুর্ভূজ, বহুভূজ বা ত্রিভুজের কোনো
একটি বাহুকে বাহিরের দিকে বর্ধিত করলে বহিঃস্থ বা বাহিরে যে কোণ উৎপন্ন হয়, তাকে
বহিঃস্থ কোণ বলে।

|
| বহিঃস্থ কোণ |
৩. বিপরীত কোণ : কোনো শেফ বা ক্ষেত্রের একটি কোণের উল্টো
বা বিপরীত দিকে অবস্থিত কোণকে সেই কোণের বিপরীত কোণ বলে।

|
| বিপরীত কোণ |
চ. অন্যান্য প্রকারভেদ : উপরে উল্লেখিত প্রকারভেদ সমূহ ছাড়াও কোণের আরও
কতকগুলো প্রকারভেদ আছে। নিম্নে সেগুলো উল্লেখ করা হল—
১. বিপ্রতীপ কোণ : কোনো রেখা পরস্পরকে কোনো বিন্দুতে ছেদ করলে ছেদ বিন্দুর
বিপরীত পাশে কোণ উৎপন্ন হয়। কোণের বাহুদ্বয়ের বিপরীত রশ্মি দুইটি যে কোণ উৎপন্ন
করে, তাদের একটিকে অপরটির বিপ্রতীপ কোণ বলে। বিপ্রতীপ কোণ পরস্পর সমান হয়।

|
|
বিপরীত কোণ |
২. প্রবৃদ্ধ কোণ : দুই সমকোণ অর্থাৎ ১৮০° থেকে বড় এবং চার সমকোণ অর্থাৎ
৩৬০° থেকে ছোট কোণকে প্রবৃদ্ধ কোণ বলে।

|
| প্রবৃদ্ধ কোণ |
৩. কেন্দ্রস্থ কোণ : কোন বৃত্তচাপের প্রান্তদ্বয় হতে সৃষ্ট ২টি সরলরেখা
বৃত্তের কেন্দ্রে মিলিত হলে যে কোণ তৈরি করে, তাকে কেন্দ্রস্থ কোণ বলে। অর্থাৎ
সহজ ভাষায় বললে, বৃত্তের কেন্দ্রে উৎপন্ন কোণকে কেন্দ্রস্থ কোণ

|
| কেন্দ্রস্থ কোণ |
৪. বৃত্তস্থ কোণ : কোনো বৃত্ত বৃত্তের অভ্যন্তরে বা পরিধির উপর যে কোণ
তৈরি করে, তাকে বৃত্তস্থ কোণ বলে।
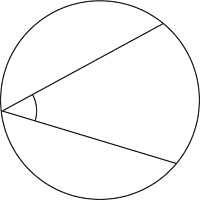
|
| বৃত্তস্থ কোণ |
৫. বন্ধন কোণ : অনুর দুটি বন্ধন দৈর্ঘ্যের মধ্যস্থিত কোণকে বন্ধন কোণ
বলে।

|
| $NH_3$ বা অ্যামোনিয়াতে বন্ধন কোণ $107^\circ$ |
নোট : যৌগিক পদার্থের ক্ষুদ্রতম কণাকে মূলত অনু বলে। পদার্থের এই
ক্ষুদ্রতম কণাসমূহ একে অপরের সাথে আঠার মতন করে লেগে থাকে। এবং তারা এক ধরনের
বন্ধনে আবদ্ধ থাকে। এই আবদ্ধ অবস্থায় তারা যে কোণ উৎপন্ন করে, তাকেই মূলত বন্ধন
কোণ বলে।
৬. স্পর্শ কোণ : কোন কঠিন সাথে যখন কোনো তরল পদার্থের স্পর্শ ঘটে, তখন
তাদের স্পর্শতলে এক ধরনের কোণের উদ্ভব হয় আর এই কোণকেই স্পর্শ কোণ বলে।

|
| চিত্রে $\angle AOC$ একটি স্পর্শ কোণ |
নোট : কঠিন পদার্থ বলতে পলিথিন, কচুপাতা এবং তরল পদার্থ বলতে পানি, তেল
ইত্যাদি বুঝায়।
৭. উন্নতি কোণ : একটি সমকোণী ত্রিভুজ তার ভূমি থেকে যে কোণ উৎপন্ন করে,
তাকে উন্নতি কোণ বলে।

|
| উন্নতি কোণ |
৮. অবনতি কোণ : একটি সমকোণী ত্রিভুজের শীর্ষ বিন্দু থেকে ভূমির সমান্তরালে
কোনো রেখা কল্পনা করলে সেই কল্পনাকৃত রেখা ও ত্রিভূজের অতিভুজ যে কোণ উৎপন্ন করে
তাকে অবনতি কোণ বলে।

|
|
অবনতি কোণ |
কোণ (Angle) সম্পর্কে আজকের আলোচনা এখানেই শেষ করছি। আশা করছি পুরো পোষ্ট পড়ার পর
কোণ নিয়ে আপনার সকল কনফিউশান কেটে যাবে। আপডেট এবং পরবর্তী কনটেন্ট পড়তে সাথে
থাকুন। থ্যাংকু।


