গণিত : ভগ্নাংশ সমস্যা সমাধান - ১

গাণিতিক যুক্তি

ভগ্নাংশ

পার্ট - ১

• ভগ্নাংশ সমস্যার সমাধান - ১
• ভগ্নাংশ সমস্যার সমাধান - ২

 ১.৪.১  ২০ ফুট লম্বা একটি বাঁশকে এমন ভাবে কেটে দু’ভাগ করা হলো যেন ছোট অংশটি বড় অংশের দুই তৃতীয়াংশ হয়, ছোট অংশের দৈর্ঘ্য কত ফুট?

(ক) ৬ ফুট

(খ) ৫ ফুট

(গ) ৭ ফুট

(ঘ) ৮ ফুট

সমাধান

উত্তর : (ঘ) ৮ ফুট

ধরি, বড় অংশটি “ক” ফুট
$\therefore$ ছোট অংশটি ক এর $\left(\frac{২}{৩}\right)$ অংশ বা $\frac{২ক}{৩}$ অংশ।
প্রশ্নমতে, ক+$\frac{২ক}{৩}$ = ২০

$\frac{৩ক+২ক}{৩}$ = ২০

৫ক = ৬০

ক = $\frac{৬০}{৫}$

$\therefore$ ক = ১২ অর্থাৎ বড় অংশটির দৈর্ঘ্য ১২ ফুট,
$\therefore$ ছোট অংশটির দৈর্ঘ্য $\frac{২\times১২}{৩}$ = ৮ ফুট

 ১.৪.২  ৩৫ ফুট লম্বা একটি বাঁশকে এমন ভাবে দু ভাগ করা হলো যেন ছোট অংশটি সম্পূর্ণ বাঁশটির $\frac{২}{৭}$ অংশ হয়। ছোট অংশের দৈর্ঘ্য কত ফুট? আবার বড় অংশটির দৈর্ঘ্য কত হবে?

(ক) ১০ ফুট; ২৫ ফুট

(খ) ২৫ ফুট; ৩০ ফুট

(গ) ১৫ ফুট; ২০ ফুট

(ঘ) ১০ ফুট; ২০ ফুট

সমাধান

উত্তর : (ক) ১০ ফুট; ২৫ ফুট

ধরি, মোট অংশ “ক” ফুট
$\therefore$ ছোট অংশটি ক এর $\frac{২}{৭}$ অংশ বা $\frac{২ক}{৭}$ অংশ।
বড় অংশটি = $\left(ক-\frac{২ক}{৭}\right)$ = $\frac{৭ক-২ক}{৭}$ = $\frac{৫ক}{৭}$ অংশ।

প্রশ্নমতে, $\frac{৫ক}{৭}+\frac{২ক}{৭}$ = ৩৫

বা, $\frac{৭ক}{৭}$ = ৩৫

বা, ক = ৩৫

$\therefore$ ছোট অংশটির দৈর্ঘ্য $\frac{২ক}{৭}$ অংশ = $\frac{২ \times ৩৫}{৭}$ = ১০ ফুট।

এবং ছোট অংশটির দৈর্ঘ্য $\frac{৫ক}{৭}$ অংশ = $\frac{৫ \times ৩৫}{৭}$ = ২৫ ফুট।

 ১.৪.৩  ২৫ ফুট লম্বা একটি বাঁশকে এমনভাবে কাঁটা হলো যে এক অংশ অন্য অংশের $\frac{১}{৪}$ হয়। ছোট অংশটির দৈর্ঘ্য কত হবে?

(ক) ৪ ফুট

(খ) ৬ ফুট

(গ) ৫ ফুট

(ঘ) ৭ ফুট

সমাধান

উত্তর : (গ) ৫ ফুট

এক অংশ অন্য অংশের ৪ ভাগের ১ অংশ। বাঁশটি কারটার পর দুই ভাগ হলো। যার প্রথম অংশকে যদি ৪ ভাগ করি, তার এক ভাগ পরিমাণ হবে দ্বিতীয় অংশ। তাহলে প্রথম ভাগে আছে ৪ অংশ এবং দ্বিতীয় ভাগে আছে ১ অংশ। মোট বাঁশটি ৫ অংশে ভাগ করা যায়। তাহলে প্রতি অংশের বা ১ অংশের দৈর্ঘ্য হলো (২৫ ফুট $\div$ ৫) = ৫ ফুট। তাহলে বাঁশটির ছোট অংশ যেহেতু এক অংশ তাই তার দৈর্ঘ্য হলো ৫ ফুট।

 ১.৪.৪  ৫ ফুট দীর্ঘ একটি তারকে এমনভাবে দু ভাগে ভাগ করা হলো যেন এক অংশ অন্য অংশের $\frac{২}{৩}$ হয়। ছোট অংশটি কত ইঞ্চি লম্বা?

(ক) ২৪ ইঞ্চি

(খ) ১২ ইঞ্চি

(গ) ১৫ ইঞ্চি

(ঘ) ১৬ ইঞ্চি

সমাধান

উত্তর : (ক) ২৪ ইঞ্চি

তারটিকে দুই টুকরা করার পর প্রথম টুকরার তিন অংশের দুই অংশ পরিমাণ হলো দ্বিতীয় টুকরা। অর্থাৎ তারটি মোট ৫ অংশে ভাগ করা যায় এবং প্রশ্নে দেওয়া আছে তারটি ৫ ফুট। অর্থাৎ ১ অংশ = ১ ফুট। এবং ছোট টুকরাটি ২ অংশ, মানে ২ ফুট। ১ ফুট = ১২ ইঞ্চি। ২ ফুট = ২ $\times$ ১২ = ২৪ ইঞ্চি।

 ১.৪.৫  একটি খুঁটির ১৫ ভাগের ৩ ভাগ ৪.৫ ফুট লম্বা হলে খুঁটিটি মোট কত ফুট লম্বা?

(ক) ৩০ ফুট

(খ) ৬৭.৫ ফুট

(গ) ২২.৫ ফুট

(ঘ) ৪৫ ফুট

সমাধান

উত্তর : (গ) ২২.৫ ফুট

৩ ভাগের মান ৪.৫ ফুট
মানে, ১ ভাগের মান ১.৫ ফুট
$\therefore$ ১৫ ভাগের মান ১৫ $\times$ ১.৫ = ২২.৫ ফুট

বিকল্প সমাধান
$\frac{৩}{১৫}$ ভাগ বা অংশ = ৪.৫ ফুট
১ ভাগ বা সম্পূর্ণ অংশ = $৪.৫ \times \frac{১৫}{৩}$ = ২২.৫ ফুট

 ১.৪.৬  কোন দোকানদার ২৬০ কেজি চালের $\frac{৩}{৫}$ অংশ বিক্রয় করে অবশিষ্ট্য চাল চার ভাগে ভাগ করে রেখে দিল। প্রতি ভাগে কত কেজি চাল রাখল?

(ক) ১৫৬ কেজি

(খ) ১০৪ কেজি

(গ) ২৬ কেজি

(ঘ) ৫২ কেজি

সমাধান

উত্তর : (গ) ২৬ কেজি

২৬০ কেজি এর $\frac{৩}{৫}$ = ১৫৬ কেজি
অর্থাৎ ১৫৬ কেজি চাল বিক্রি করে দিলেন।
সুতরাং অবশিষ্ট্য চাল থাকে (২৬০-১৫৬) = ১০৪ কেজি
১০৪ কেজি চালকে চার ভাগ করলে প্রতি ভাগে হয় ১০৪ $\div$ ৪ = ২৬ কেজি।

 ১.৪.৭  একটি শ্রেণিতে মোট ৬০ জন শিক্ষার্থী রয়েছে যাদের মধ্যে $\frac{২}{৫}$ অংশ ছাত্র। ঐ শ্রেণিতে ছাত্রীর সংখ্যা কত জন?

(ক) ২৪ জন

(খ) ৩৬ জন

(গ) ১২ জন

(ঘ) ২০ জন

সমাধান

উত্তর : (খ) ৩৬ জন

ছাত্র = ৬০ এর $\frac{২}{৫}$ অংশ = ২৪ জন।
$\therefore$ ছাত্রী = ৬০-২৪=৩৬ জন।

 ১.৪.৮  একটি গরু ৪৫০ টাকায় বিক্রয় করায় তার ক্রয়মূল্যের $\frac{১}{৮}$ অংশ লাভ হয়। গরুটির ক্রয়মূল্য কত?

(ক) ৪৫০ টাকা

(খ) ৪২০ টাকা

(গ) ৫০০ টাকা

(ঘ) ৪০০ টাকা

সমাধান

উত্তর : (ঘ) ৪০০ টাকা

ক্রয়মূল্য ৮ অংশ ও লাভ ১ অংশ।
সুতরাং বিক্রয় মূল্য ৯ অংশ।

বিক্রয়মূল্য, ৯ অংশ = ৪৫০ টাকা
১ অংশ = ৪৫০ $\div$ ৯ = ৫০ টাকা
ক্রয়মূল্য, ৮ অংশ = ৫০ $\times$ ৮ = ৪০০ টাকা।

বিকল্প সমাধান - ১
লাভে বিক্রি = ৮+১ = ৯ টাকা
তাহলে ক্রয়মূল্য = ৯-১ = ৮ টাকা [যেহেতু ৯ টাকা বা মোট অংশের মধ্যে ক্রয় এবং বিক্রয় উভয়ই আছে]

নির্দিষ্ট টাকা লাভ করার পর,
বিক্রয় মূল্য ৯ টাকা হলে ক্রয়মূল্য ৮ টাকা
বিক্রয় মূল্য ১ টাকা হলে ক্রয়মূল্য $\frac{৮}{৯}$ টাকা
বিক্রয় মূল্য ৪৫০ টাকা হলে ক্রয়মূল্য $\frac{৮ \times ৪৫০}{৯}$ = ৪০০ টাকা

বিকল্প সমাধান - ২
ধরি, ক্রয়মূল্য = ‘ক’ টাকা
লাভ = ক্রয়মূল্যের $\frac{১}{৮}$ অংশ
= ক এর $\frac{১}{৮}$ অংশ
= $\frac{ক}{৮}$

প্রশ্ন মতে,

ক্রয়মূল্য + লাভ = বিক্রয়মূল্য

বা, ক + $\frac{ক}{৮}$ = ৪৫০

বা, $\frac{৮ক+ক}{৮}$ = ৪৫০

বা, $\frac{৯ক}{৮}$ = ৪৫০

বা, ক = $৪৫০ \times \frac{৮}{৯}$

$\therefore$ ক = ৪০০
অর্থাৎ ক্রয়মূল্য ‘ক’ = ৪০০ টাকা।

 ১.৪.৯  ২৪০ টি আমের একটি ঝুড়ি কিনে দেখা গেল যে মোট আমের $\frac{১}{১৬}$ অংশ পঁচে গেছে। ঝুড়িতে মোট কতটি ভালো আম আছে?

(ক) ২২৫ টি

(খ) ২০০ টি

(গ) ১৫ টি

(ঘ) ৪০ টি

সমাধান

উত্তর : (ক) ২২৫ টি

$\frac{১}{১৬}$ যদি পঁচে যায়, তাহলে নিশ্চয় ভালো আছে $\frac{১৫}{১৬}$ অংশ
$\therefore$ ভালো আছে ২৪০ এর $\frac{১৫}{১৬}$ = ২২৫ টি আম

বিকল্প সমাধান - ১
ধরি, মোট আম ১ অংশ
ভালো আমের পরিমাণ $\left(১-\frac{১}{১৬}\right)$ = $\frac{১৫}{১৬}$ অংশ
$\therefore$ ভালো আছে ২৪০ এর $\frac{১৫}{১৬}$ = ২২৫ টি আম

বিকল্প সমাধান - ২
পঁছে গেছে ২৪০ এর $\frac{১}{১৬}$ = ১৫ টি আম
$\therefore$ ভালো আছে = ২৪০-১৫ = ২২৫ টি আম

 ১.৪.১০  কোন পুস্তকের ৯৬ পৃষ্ঠা পড়ার পরেও তার $\frac{৫}{১৩}$ অংশ পড়তে বাকী থাকলে, পুস্তকটির মোট পৃষ্ঠা সংখ্যা কত?

(ক) ১০৪ পৃষ্ঠা

(খ) ১৫০ পৃষ্ঠা

(গ) ২৫৬ পৃষ্ঠা

(ঘ) ১৫৬ পৃষ্ঠা

সমাধান

উত্তর : (ঘ) ১৫৬ পৃষ্ঠা

$\frac{৫}{১৩}$ অংশ পড়া বাকী, অর্থাৎ পড়া শেষ $\frac{৮}{১৩}$ অংশ
$\frac{৮}{১৩}$ অংশ = ৯৬ পৃষ্ঠা
১ বা সম্পূর্ণ অংশ = $৯৬ \times \frac{১৩}{৮}$ = ১৫৬ পৃষ্ঠা

বিকল্প সমাধান
ধরি, মোট পৃষ্ঠা সংখ্যা ১ অংশ
$\therefore$ পড়া শেষ হয়েছে $\left(১-\frac{৫}{১৩}\right)$ = $\frac{৮}{১৩}$ অংশ

প্রশ্নমতে,
$\frac{৮}{১৩}$ অংশ = ৯৬ পৃষ্ঠা
$\therefore$ ১ বা সম্পূর্ণ অংশ = $\frac{৯৬ \times ১৩}{৮}$ = ১৫৬ পৃষ্ঠা

 ১.৪.১১  কোন কর্মচারী মূল বেতনের $\frac{১}{৪০}$ ভাগের সমপরিমাণ বিশেষ ভাতা পান। তার বিশেষ ভাতা ৪০ টাকা হলে, মূল বেতন কত টাকা?

(ক) ১২০০ টাকা

(খ) ১৪০০ টাকা

(গ) ১৬০০ টাকা

(ঘ) ১৮০০ টাকা

সমাধান

উত্তর : (গ) ১৬০০ টাকা

$\frac{১}{৪০}$ ভাগ = ৪০ টাকা
$\therefore$ ১ ভাগ = ৪০ $\times$ ৪০ = ১৬০০ টাকা।

 ১.৪.১২  এক ব্যক্তি তার মোট সম্পত্তির $\frac{৩}{৭}$ অংশ ব্যয় করার পরে অবশিষ্টের $\frac{৫}{১২}$ অংশ ব্যয় করে দেখলেন যে তার নিকট ১০০০ টাকা রয়েছে। তার মোট সম্পত্তির মূল্য কত?

(ক) ২০০০ টাকা

(খ) ২৩০০ টাকা

(গ) ২৫০০ টাকা

(ঘ) ৩০০০ টাকা

সমাধান

উত্তর : (ঘ) ৩০০০ টাকা

ধরি, সম্পূর্ণ অংশ = ১ অংশ
$\frac{৫}{১২}$ অংশ ব্যয় করার পরে অবশিষ্ট থাকে $\left(১-\frac{৩}{৭}\right)$ = $\frac{৪}{৭}$

দ্বিতীয়বার ব্যয় করেন অবশিষ্টের $\frac{৫}{১২}$ অংশ
$\therefore$ দ্বিতীয় ব্যয় = $\frac{৪}{৭}$ এর $\frac{৫}{১২}$ অংশ = $\frac{২০}{৮৪}$ বা $\frac{৫}{২১}$ অংশ

প্রশ্নমতে,
$\frac{৪}{৭}$ অংশ - $\frac{৫}{২১}$ অংশ = ১০০০
$\frac{১২-৫}{২১}$ অংশ = ১০০০
$\frac{৭}{২১}$ অংশ = ১০০০
১ অংশ = $১০০০ \times \frac{২১}{৭}$ = ৩০০০ টাকা

 ১.৪.১৩  এক ব্যক্তি তার আয়ের $\frac{১}{৩}$ অংশের পরিবর্তে $\frac{১}{৪}$ অংশ ব্যয় করলে তার ২০০ টাকা কম খরচ হতো। তার আয় কত?

(ক) ২৮০০ টাকা

(খ) ২৬০০ টাকা

(গ) ২৫০০ টাকা

(ঘ) ২৪০০ টাকা

সমাধান

উত্তর : (ঘ) ২৪০০ টাকা

$\frac{১}{৩}$ - $\frac{১}{৪}$ = $\frac{১}{১২}$
প্রশ্নমতে, $\frac{১}{১২}$ অংশ = ২০০ টাকা
$\therefore$ ১ অংশ = ২০০ $\times$ ১২ = ২৪০০ টাকা

 ১.৪.১৪  এক ব্যক্তি মাসিক বেতনের $\frac{১}{৪০}$ অংশ মহার্ঘভাতা পান। তার মাসিক বেতন ১৬০০ টাকা হলে, তার মহার্ঘভাতা কত?

(ক) ৩০ টাকা

(খ) ৪০ টাকা

(গ) ৬৪ টাকা

(ঘ) ৮০ টাকা

সমাধান

উত্তর : (খ) ৪০ টাকা

১৬০০ এর $\frac{১}{৪০}$ = ৪০ টাকা

 ১.৪.১৫  কোন সংখ্যার $\frac{২}{৭}$ অংশ ৬৪ এর সমান?

(ক) ১৮$\frac{২}{৭}$

(খ) ২৪৮

(গ) ২১৭

(ঘ) ২২৪

সমাধান

উত্তর : (ঘ) ২২৪

ধরি, ক এর $\frac{২}{৭}$ = ৬৪
বা, ক = ৬৪ $\times \frac{৭}{২}$ = ২২৪

 ১.৪.১৬  সবচেয়ে বড় সংখ্যা কোনটি?

(ক) ০.০০৯৯

(খ) ০.১

(গ) $\frac{৯}{১০০}$

(ঘ) $\frac{৯}{১০০০}$

সমাধান

উত্তর : (খ) ০.১

প্রশ্নের অপশন সবগুলোকে দশমিকে রূপান্তর করি এবং স্থানাঙ্ক সংখ্যা একই করি অতঃপর প্রত্যেকের দশমিকের আগে যদি শূন্য পাই তবে কাল্পনিক ভাবে দশমিক বাদ দিলে কত হয় দেখি।

(ক) ০.০০৯৯ কাল্পনিক ভাবে দশমিক বাদ দিলে হয় ৯৯

(খ) ০.১ = ০.১০০০ কাল্পনিক ভাবে দশমিক বাদ দিলে হয় ১০০০

(গ) $\frac{৯}{১০০}$ = ০.০৯ = ০.০৯০০ কাল্পনিক ভাবে দশমিক বাদ দিলে হয় ৯০০

(ঘ) $\frac{৯}{১০০০}$ = ০.০০৯ = ০.০০৯০ কাল্পনিক ভাবে দশমিক বাদ দিলে হয় ৯০

সুতরাং দেখা যাচ্ছে অপশন খ’ই সব থেকে বড়।

 ১.৪.১৭  ১ ঘণ্টা ২০ মিনিট, ৪ ঘণ্টার কত অংশ?

(ক) $\frac{১}{৩}$ অংশ

(খ) $\frac{৩}{১১}$ অংশ

(গ) $\frac{২}{১৩}$ অংশ

(ঘ) $\frac{৪}{১৫}$ অংশ

সমাধান

উত্তর : (ক) $\frac{১}{৩}$ অংশ

১ ঘন্টা ২০ মিনিট = ৬০ + ২০ = ৮০ মিনিট
৪ ঘণ্টা = ৬০ $\times$ ৪ = ২৪০ মিনিট
অংশ = $\frac{৮০}{২৪০}$ = $\frac{১}{৩}$ অংশ

 ১.৪.১৮  কোনটি সবচেয়ে ছোট?

(ক) $\frac{২}{১১}$

(খ) $\frac{৩}{১১}$

(গ) $\frac{২}{১৩}$

(ঘ) $\frac{৪}{১৫}$

সমাধান

উত্তর : (গ) $\frac{২}{১৩}$

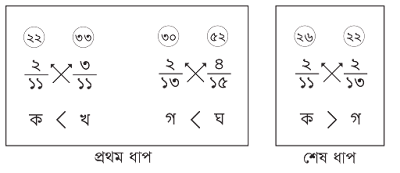
উপরের চিত্রের মত ভগ্নাংশ ক ও খ এর হর ও লবগুলো গুণ করে উপরে লিখতে হবে এবং গুণফলগুলোর মধ্যে তুলনা করে কে বড় কে ছোট তা নির্ণয় করতে হবে। একই ভাগে ভগ্নাংশ গ ও ঘ তুলনা করতে হবে।
এখন যেহেতু প্রশ্নে ছোট ভগ্নাংশ কোনটি তা নির্ণয় করতে বলা হয়েছে, তাই ক ও খ থেকে যেটি ছোট, তার সাথে গ ও ঘ এর মধ্যে যেটি ছোট তাদের মধ্যে তুলনা করে আবার ছোটটি নির্ণয়া করতে হবে। শেষ ধাপে যে ভগ্নাংশটি ছোট পাওয়া গেল সেটিই সবগুলো ভগ্নাংশের মধ্যে ছোট।
একই প্রকৃয়ায় সবচেয়ে বড় ভগ্নাংশও নির্ণয় করা যায়।

 ১.৪.১৯  নিম্ন বর্ণিত ভগ্নাংশের কোনটি $\frac{১}{২}$ এর চেয়ে বেশি, বা $\frac{১}{২}$ থেকে বড়?

(ক) $\frac{৭}{১৫}$

(খ) $\frac{৩০}{৬১}$

(গ) $\frac{৩১}{৬১}$

(ঘ) কোনটি নয়

সমাধান

উত্তর : (গ) $\frac{৩১}{৬১}$

সূত্র : $\frac{১}{২}$ এর সাথে হর গুণ করতে হবে এবং ফলাফল লব থেকে ছোট হতে হবে।

(ক) এর ক্ষেত্রে $\frac{১}{২} \times ১৫$ = ৭.৫০ যা লব ৭ থেকে বড়। $\therefore$ এটি গ্রহণযোগ্য নয়।

(খ) এর ক্ষেত্রে $\frac{১}{২} \times ৬১$ = ৩০.৫০ যা লব ৩০ থেকে বড়। $\therefore$ এটি গ্রহণযোগ্য নয়।

(গ) এর ক্ষেত্রে $\frac{১}{২} \times ৬১$ = ৩০.৫০ যা লব ৩১ থেকে ছোট। $\therefore$ এটি গ্রহণযোগ্য।

বিকল্প সমাধান
$\frac{১}{২}$ বড় হলে হবে না, $\frac{১}{২}$ থেকে বড় হতে হবে।

 ১.৪.২০  কোন ভগ্নাংশটি $\frac{২}{৩}$ থেকে বড়?

(ক) $\frac{৩৩}{৫০}$

(খ) $\frac{৮}{১১}$

(গ) $\frac{৩}{৫}$

(ঘ) $\frac{১৩}{২৭}$

সমাধান

উত্তর : (খ) $\frac{৮}{১১}$

সূত্র : $\frac{২}{৩}$ এর সাথে হর গুণ করতে হবে এবং ফলাফল লব থেকে ছোট হতে হবে।

(ক) এর ক্ষেত্রে $\frac{২}{৩} \times ৫০$ = ৩৩.৩৩ যা লব ৩৩ থেকে বড়। $\therefore$ এটি গ্রহণযোগ্য নয়।

(খ) এর ক্ষেত্রে $\frac{২}{৩} \times ১১$ = ৭.৩৩ যা লব ৮ থেকে ছোট। $\therefore$ এটি গ্রহণযোগ্য।

(গ) এর ক্ষেত্রে $\frac{২}{৩} \times ৫$ = ৩.৩৩ যা লব ২ থেকে বড়। $\therefore$ এটি গ্রহণযোগ্য নয়।

(ঘ) এর ক্ষেত্রে $\frac{২}{৩} \times ২৭$ = ১৮ যা লব ১৩ থেকে বড়। $\therefore$ এটি গ্রহণযোগ্য নয়।

 ১.৪.২১  যদি $\frac{১৭}{২৪}$, $\frac{১}{২}$, $\frac{৩}{৮}$, $\frac{৩}{৪}$ এবং $\frac{৯}{১৬}$ সংখ্যাগুলো বৃহত্তম হতে ক্ষুদ্রতম ভাবে সাজানো হয়, তাহলে মাঝখানের ভগ্নাংশ কোনটি হবে?

(ক) $\frac{১৭}{২৪}$

(খ) $\frac{১}{২}$

(গ) $\frac{৩}{৮}$

(ঘ) $\frac{৩}{৪}$

(ঙ) $\frac{৯}{১৬}$

সমাধান

উত্তর : (ঙ) $\frac{৯}{১৬}$

ভগ্নাংশগুলোর হরদ্বয়ের ল.সা.গু. ৪৮

প্রথম ভগ্নাংশের ক্ষেত্রে,
৪৮$\div$২৪ = ২, $\frac{১৭\times২}{২৪\times২}$ = $\frac{৩৪}{৪৮}$

দ্বিতীয় ভগ্নাংশের ক্ষেত্রে,
৪৮$\div$২ = ২৪, $\frac{১\times২৪}{২\times২৪}$ = $\frac{২৪}{৪৮}$

তৃতীয় ভগ্নাংশের ক্ষেত্রে,
৪৮$\div$৮ = ৬, $\frac{৩\times৬}{৮\times৬}$ = $\frac{১৮}{৪৮}$

চতুর্থ ভগ্নাংশের ক্ষেত্রে,
৪৮$\div$৪ = ১২, $\frac{৩\times১২}{৪\times১২}$ = $\frac{৩৬}{৪৮}$

পঞ্চম ভগ্নাংশের ক্ষেত্রে,
৪৮$\div$১৬ = ৩, $\frac{৯\times৩}{১৬\times৩}$ = $\frac{২৭}{৪৮}$

বৃহত্তম থেকে ভগ্নাংশগুলো সাজালে পাই, $\frac{৩৬}{৪৮}$ > $\frac{৩৪}{৪৮}$ > $\frac{২৭}{৪৮}$ > $\frac{২৪}{৪৮}$ > $\frac{১৮}{৪৮}$
বা, $\frac{৩}{৪}$ > $\frac{১৭}{২৪}$ > $\frac{৯}{১৬}$ > $\frac{১}{২}$ > $\frac{৩}{৮}$
অর্থাৎ, মাঝের ভগ্নাংশটি হলো $\frac{৯}{১৬}$

 ১.৪.২২  একটি ভগ্নাংশের লব ও হরের পার্থক্য ১ এবং সমষ্টি ৭, তাহলে ভগ্নংশটি কোন?

(ক) $\frac{৪}{৩}$

(খ) $\frac{৩}{৪}$

(গ) $\frac{৫}{৬}$

(ঘ) $\frac{৬}{৫}$

সমাধান

উত্তর : (ক) $\frac{৪}{৩}$

ধরি, লব = X ও হর = Y, $\therefore$ ভগ্নাংশটি = $\frac{X}{Y}$

প্রশ্নমতে, X-Y=1 ---($i$)
এবং X+Y=7 ---($ii$)

সমীকরণ ($i$) + ($ii$) হলে,
(X-Y) + (X+Y) = 1 + 7
বা, X-Y+X+Y=8
বা, 2X=8
$\therefore$ X=4

X এর মান ($ii$) নং সমীকরণে বসিয়ে পাই,
বা, 4+Y=7
$\therefore$ Y=7-4 =3

অর্থাৎ ভগ্নাংশটি = $\frac{X}{Y}$ = $\frac{4}{3}$

 ১.৪.২৩  কোনো ভগ্নাংশের লবের সাথে ৩ যোগ করলে এর মান ১ এবং হরের সাথে ২ যোগ করলে মান $\frac{১}{২}$ হয়। ভগ্নাংশটি নির্ণয় করুন।

(ক) $\frac{৪}{৭}$

(খ) $\frac{৫}{৮}$

(গ) $\frac{৮}{১১}$

(ঘ) $\frac{৭}{১০}$

সমাধান

উত্তর : (খ) $\frac{৫}{৮}$

মনে করি, ভগ্নাংশটি $\frac{x}{y}$
$\therefore \frac{x+৩}{y} = ১$
বা, x+৩=y
বা, x-y=-3 .....($i$)

এবং $\frac{x}{y+২}=\frac{১}{২}$
বা, ২x=y+২ .....($ii$)

($i$)নং ($ii$) নং সমীকরণ বিয়োগ করি
(x-y)-(২x-y)=-৩-২
বা, x-y-২x+y=-৫
বা, -x=-৫
$\therefore$ x=৫

x=৫ ($i$) নং এ বসাই
৫-y=-৩
বা, -y=-৩-৫
বা, -y=-৮
$\therefore$ y=৮

$\therefore$ ভগ্নাংশটি $\frac{x}{y}$ = $\frac{৫}{৮}$

 ১.৪.২৪  কোন সংখ্যার $\frac{১}{২}$ অংশের সাথে ৬ যোগ করলে সংখ্যাটির $\frac{২}{৩}$ অংশ হবে। সংখ্যাটি কত?

(ক) ৩৫

(খ) ৫২

(গ) ২৩

(ঘ) ৩৬

সমাধান

উত্তর : (ঘ) ৩৬

ধরি সংখ্যাটি “ক”

প্রশ্নমতে,
ক এর $\frac{১}{২}$ + ৬ = ক এর $\frac{২}{৩}$
বা, $\frac{ক}{২}+৬$ = $\frac{২ক}{৩}$
বা, $\frac{ক+১২}{২}$ = $\frac{২ক}{৩}$
বা, ৩ক + ৩৬ = ৪ক
বা, ৩ক - ৪ক = -৩৬
বা, -ক = -৩৬
$\therefore$ ক = ৩৬

 ১.৪.২৫  কোনো সংখ্যার তিন অষ্টমাংশের সাথে এর দ্বিগুণের দুই পঞ্চমাংশ যোগ করলে যা হয় তা মূল সংখ্যাটি থেকে ২১ বেশি। সংখ্যাটির তিন পঞ্চমাংশ কত?

(ক) ১৫০

(খ) ১২০

(গ) ১০০

(ঘ) ৭২

(ঙ) কোনোটিই নয়

সমাধান

উত্তর : (ঘ) ৭২

মনে করি, সংখ্যাটি x
$\therefore$ $\frac{৩ক}{৮}+২x\times\frac{২}{৫}$ = X + ২১
বা, $\frac{৩ক}{৮} + \frac{৪ক}{৫}$ = x + ২১
বা, ১৫x+৩২x = ৪০x + ৮৪০ [৪০ দ্বারা গুণ করে]
বা, ৪৭x - ৪০x = ৮৪০
বা, ৭x = ৮৪০
বা, x = $\frac{৮৪০}{৭}$=১২০
$\therefore$ সংখ্যাটির তিন পঞ্চমাংশ = ১২০ এর $\times \frac{৩}{৫}$ = ৭২

- ১ -